题目内容
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 10 | |
| [39.97,39.99) | 20 | |
| [39.99,40.01) | 50 | |
| [40.01,40.03] | 20 | |
| 合计 | 100 |
(2)若以上述频率作为概率,已知标准乒乓球的直径为40.00mm,试求这批乒乓球的直径误差不超过0.03mm的概率;
(3)(仅文科生做)据直方图估计这批乒乓球直径的众数;
(4)(仅理科生做)据直方图估计这批乒乓球直径的中位数和平均数(结果保留三位小数).
考点:频率分布直方图,频率分布表,众数、中位数、平均数
专题:概率与统计
分析:(1)根据所给的频数和样本容量,用频数除以样本容量做出每一组数据对应的频率,填入表中,画出对应的频率分步直方图;
(2)误差不超过0.03mm,即直径落在[39.97,40.03]范围内,将直径落在[39.97,40.03]范围内的频率求和即可得到所求;
(3)根据众数是频率分布直方图中最高矩形的底边中点的横坐标可求出所求;
(4)做出每一组数据的区间的中点值,用这组数据的中间值分别乘以对应的这个区间的频率,得到这组数据的总体平均值,中位数出现在概率是0.5的地方.
(2)误差不超过0.03mm,即直径落在[39.97,40.03]范围内,将直径落在[39.97,40.03]范围内的频率求和即可得到所求;
(3)根据众数是频率分布直方图中最高矩形的底边中点的横坐标可求出所求;
(4)做出每一组数据的区间的中点值,用这组数据的中间值分别乘以对应的这个区间的频率,得到这组数据的总体平均值,中位数出现在概率是0.5的地方.
解答:
解:(1)频率分布表如下:
频率分布直方图如下:
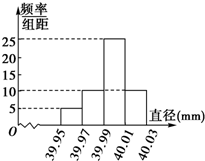
(2)误差不超过0.03mm,即直径落在[39.97,40.03]范围内,其概率为0.2+0.5+0.2=0.9,
(3)(文科)数据的众数是40.00 (mm),
(4)(理科)数据的中位数为39.990+0.2/25=39.998(mm),
平均数约为39.96×0.10+39.98×0.20+40.00×0.50+40.02×0.20=39.996(mm).
| 分组 | 频数 | 频率 |
| [39.95,39.97) | 10 | 0.10 |
| [39.97,39.99) | 20 | 0.20 |
| [39.99,40.01) | 50 | 0.50 |
| [40.01,40.03) | 20 | 0.20 |
| 合计 | 100 | 1 |

(2)误差不超过0.03mm,即直径落在[39.97,40.03]范围内,其概率为0.2+0.5+0.2=0.9,
(3)(文科)数据的众数是40.00 (mm),
(4)(理科)数据的中位数为39.990+0.2/25=39.998(mm),
平均数约为39.96×0.10+39.98×0.20+40.00×0.50+40.02×0.20=39.996(mm).
点评:本题考查了统计中的茎叶图,众数、中位数、平均数等基本概念.众数是指在这组数据中出现次数最多的一个数,中位数是指将数据从小到大排列,处于中间位置的数,如果中间位置有两个数,则取这两个数的平均值.频率分布直方图中小长方形的面积=组距×=频率,各个矩形面积之和等于1,能根据直方图求频率.属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 如图中三个直角三角形是一个体积为20的几何体的三视图,则h=( )
如图中三个直角三角形是一个体积为20的几何体的三视图,则h=( )| A、6 | B、8 | C、4 | D、12 |