题目内容
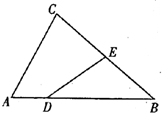如图，在△ABC中，已知点D，E分别在边AB，BC上，且AB=4AD，BC=2BE．（Ⅰ）用向量
| AB |
| AC |
| DE |
（Ⅱ）设AB=8，AC=5，A=60°，求线段DE的长．
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：（I）利用向量的三角形法则和向量共线定理即可得出；
（II）由向量的数量积性质即可得出．
（II）由向量的数量积性质即可得出．
解答：
解：（I）∵
=
+
=
+
=
+
(
-
)=
+
；
（II）由（I）可得
2=(
+
)2=
2+
2+
•
=
×82+
×52+
×8×5×cos60°
=
．
∴|
|=
．
| DE |
| DB |
| BE |
| 3 |
| 4 |
| AB |
| 1 |
| 2 |
| BC |
| 3 |
| 4 |
| AB |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 4 |
| AB |
| 1 |
| 2 |
| AC |
（II）由（I）可得
| DE |
| 1 |
| 4 |
| AB |
| 1 |
| 2 |
| AC |
| 1 |
| 16 |
| AB |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AB |
| AC |
=
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 61 |
| 4 |
∴|
| DE |
| ||
| 2 |
点评：本题考查了向量的三角形法则和向量共线定理、向量的数量积性质，属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
放在水平桌面上的某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A、π+4 | ||
| B、π+3 | ||
C、
| ||
D、
|
阅读如图所示的程序框图，则输出的S的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若将函数f（x）=sin2x+cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|