题目内容
已知数列{an}满足:
=n(n∈N*),且a4=28,则{an}的通项公式为an= .
| an+1+an-1 |
| an+1-an+1 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由已知结合数列递推式求出a1,a2,a3,归纳猜测出数列的一个通项公式,然后利用数学归纳法证明得答案.
解答:
解:由
=n(n∈N*),且a4=28,
得:
=3,解得a3=15.
再代入
=n(n∈N*),
得:
=2,解得a2=6.
同理求得a1=1,
∴a1=1=2×12-1,
a2=6=2×22-2,
a3=15=2×32-3,
a4=28=2×42-4,
由上猜测an=2n2-n.
下面由数学归纳法证明:
①当n=1时,a1=1=2×12-1成立,
②假设n=k时成立,即ak=2k2-k,
那么,当n=k+1时,
由
=n,得:
ak+1+ak-1=kak+1-kak+k,
即ak+1=
•ak-
=
•(2k2-k)-
=2(k+1)2-(k+1).
综①②所述,an=2n2-n.
故答案为:2n2-n.
| an+1+an-1 |
| an+1-an+1 |
得:
| 28+a3-1 |
| 28-a3+1 |
再代入
| an+1+an-1 |
| an+1-an+1 |
得:
| 15+a2-1 |
| 15-a2+1 |
同理求得a1=1,
∴a1=1=2×12-1,
a2=6=2×22-2,
a3=15=2×32-3,
a4=28=2×42-4,
由上猜测an=2n2-n.
下面由数学归纳法证明:
①当n=1时,a1=1=2×12-1成立,
②假设n=k时成立,即ak=2k2-k,
那么,当n=k+1时,
由
| an+1+an-1 |
| an+1-an+1 |
ak+1+ak-1=kak+1-kak+k,
即ak+1=
| k+1 |
| k-1 |
| k+1 |
| k-1 |
| k+1 |
| k-1 |
| k+1 |
| k-1 |
综①②所述,an=2n2-n.
故答案为:2n2-n.
点评:本题考查数列递推式,考查了利用归纳、猜测、然后利用数学归纳法求解数列通项公式的方法,是中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
在(1+x)3+(1+x)4+…+(1+x)50的展开式中,x3的系数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如下的2×2列联表.
则至少有( )的把握认为喜爱打篮球与性别有关.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| A、95% | B、99% |
| C、99.5% | D、99.9% |
在等差数列{an}中,已知a3+a9=16,则该数列前11项和S11=( )
| A、58 | B、88 |
| C、143 | D、176 |
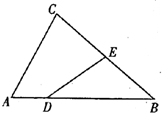 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.