题目内容

若将函数f（x）=sin2x+cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是（　　）
A、
π
8
B、
π
4
C、
3π
8
D、
3π
4
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值
分析：利用两角和的正弦函数对解析式进行化简，由所得到的图象关于y轴对称，根据对称轴方程求出φ的最小值．
解答： 解：函数f（x）=sin2x+cos2x=
2
sin（2x+
π
4
）的图象向右平移φ的单位，
所得图象是函数y=
2
sin（2x+
π
4
-2φ），
图象关于y轴对称，可得
π
4
-2φ=kπ+
π
2
，
即φ=-
kπ
2
-
π
8
，
当k=-1时，φ的最小正值是
3π
8
．
故选：C．
点评：本题考查三角函数的图象变换，考查正弦函数图象的特点，属于基础题．
练习册系列答案
相关题目
设直线x-3y+m=0（m≠0）与双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两条渐近线分别交于点A，B．若点P（m，0）满足|PA|=|PB|，则该双曲线的离心率是
 
．
执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（　　）
A、0B、1C、2D、3
已知i是虚数单位，a，b∈R，则“a=b=1”是“（a+bi）2=2i”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（　　）
A、0.8B、0.75
C、0.6D、0.45
已知P是圆x2+y2=1上的一动点，则P点到直线l：x+y-2
2
=0的距离的最大值为（　　）
A、1
B、3
C、2
D、2
2
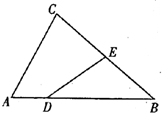如图，在△ABC中，已知点D，E分别在边AB，BC上，且AB=4AD，BC=2BE．
（Ⅰ）用向量
AB
，
AC
表示
DE
；
（Ⅱ）设AB=8，AC=5，A=60°，求线段DE的长．
已知向量
a
=（cosωx-sinωx，sinωx），
b
=（-cosωx-sinωx，2
3
cosωx）（ω＞0），函数f（x）=
a
•
b
的最小正周期为2π．
（Ⅰ）求ω的值；
（Ⅱ）将函数y=f（x）的图象上各点的横坐标缩短到原来的
1
2
倍，纵坐标不变，得到函数y=g（x）的图象，求函数y=g（x）在区间[0，
π
2
]上的取值范围．
设数列{an}的前n项和为Sn（n∈N*），关于数列{an}有下列命题：
①若{an}既是等差数列又是等比数列，则an=an+1（n∈N*）；
②若Sn=an2+bn，（a，b∈R），则{an}是等差数列；
③若Sn=1-（-1）n，则{an}是等比数列；
④若{an}是等比数列，则Sm，S2m-Sm，S3m-S2m（m∈N*）也成等比数列；
其中正确的命题是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网