题目内容
下列各结论中:
①抛物线y=
x2的焦点到直线y=x-1的距离为
;
②已知函数f(x)=xα的图象经过点(2,
),则f(4)的值等于
;
③命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x<0.
正确结论的序号是 .
①抛物线y=
| 1 |
| 4 |
| 2 |
②已知函数f(x)=xα的图象经过点(2,
| ||
| 2 |
| 1 |
| 2 |
③命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x<0.
正确结论的序号是
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①抛物线y=
x2的焦点为(0,1),利用点到直线的距离公式,可求焦点到直线y=x-1的距离;
②先求出α=-
,再计算f(4)的值;
③命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x≤0”.
| 1 |
| 4 |
②先求出α=-
| 1 |
| 2 |
③命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x≤0”.
解答:
解:①抛物线y=
x2的焦点为(0,1),到直线y=x-1的距离为
=
,正确;
②已知函数f(x)=xα的图象经过点(2,
),则2α=
,∴α=-
,∴f(4)的值等于
,正确;
③命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x≤0”,故不正确.
故答案为:①②.
| 1 |
| 4 |
| 2 | ||
|
| 2 |
②已知函数f(x)=xα的图象经过点(2,
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
③命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x≤0”,故不正确.
故答案为:①②.
点评:本题考查命题的真假判断与应用,涉及知识点多,需要逐一判断,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
阅读如图的程序框图,若输出的y=1,则输入的x的值可能是( )


A、±
| ||
B、-
| ||
C、±
| ||
| D、2 |
已知i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知P是圆x2+y2=1上的一动点,则P点到直线l:x+y-2
=0的距离的最大值为( )
| 2 |
| A、1 | ||
| B、3 | ||
| C、2 | ||
D、2
|
在(1+x)3+(1+x)4+…+(1+x)50的展开式中,x3的系数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
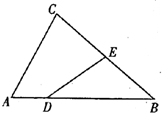 如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.
如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=4AD,BC=2BE.