题目内容
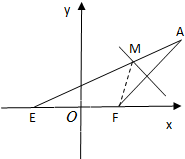 如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.
如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.(1)求点M的轨迹C1的方程;
(2)抛物线C2:y2=4x与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值.
考点:直线与圆锥曲线的综合问题,抛物线的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)判断轨迹是椭圆,求解a,b即可得到椭圆方程.
(2)利用椭圆与抛物线取得P的坐标,求出PQ的方程,利用直线方程与抛物线方程求出直线方程,然后求解抛物线的POQ弧上的点R到直线PQ的距离的最大值.
(2)利用椭圆与抛物线取得P的坐标,求出PQ的方程,利用直线方程与抛物线方程求出直线方程,然后求解抛物线的POQ弧上的点R到直线PQ的距离的最大值.
解答:
解:(1)依题意有|ME|+|MF|=|ME|+|MA|
=|AE|=4>|EF|=2
∴点M的轨迹是以E,F为焦点的椭圆.…(3分)
∵2a=4,2c=2,
∴a=2,b=
,
故所求点M的轨迹方程是
+
=1…(6分)
(2)联立方程
,可得32+16x-12=0,
解得x=
或x=-6(舍去)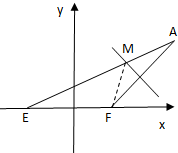
将x=
代入抛物线方程得y=
,
∴点P的坐标为(
,
)…(8分)
可得kPF=-2
,于是可得PQ所在直线的方程为:2
x+y-2
=0…(9分)
设PQ的平行线方程为:2
x+y+t=0.
由
⇒24x2+4(
-1)x+t2=0
令△=16(
t-1)2-96t2=0,解得t=
…(11分)
∵R到PQ的最大距离即为直线2
x+y+
=0与PQ之间的距离,
故所求为d=
=
…(13分)
=|AE|=4>|EF|=2
∴点M的轨迹是以E,F为焦点的椭圆.…(3分)
∵2a=4,2c=2,
∴a=2,b=
| 3 |
故所求点M的轨迹方程是
| x2 |
| 4 |
| y2 |
| 3 |
(2)联立方程
|
解得x=
| 2 |
| 3 |

将x=
| 2 |
| 3 |
2
| ||
| 3 |
∴点P的坐标为(
| 2 |
| 3 |
2
| ||
| 3 |
可得kPF=-2
| 6 |
| 6 |
| 6 |
设PQ的平行线方程为:2
| 6 |
由
|
| 6 |
令△=16(
| 6 |
| ||
| 12 |
∵R到PQ的最大距离即为直线2
| 6 |
| ||
| 12 |
故所求为d=
| ||||||
|
| 5 |
| 12 |
| 6 |
点评:本题考查抛物线与椭圆的位置关系的综合应用,直线方程与排趋性方程的关系,点到直线的距离,考查分析问题解决问题的能力.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=2y-3x的最大值为( )
|
| A、-3 | ||
| B、5 | ||
| C、2 | ||
D、
|