题目内容
已知在△ABC中,∠A=
,BC=3,求△ABC的周长(用∠B表示).
| π |
| 3 |
考点:三角形中的几何计算
专题:解三角形
分析:利用正弦定理求出三角形的外接圆的直径,然后利用B表示出b、c,即可得到三角形的周长.
解答:
解:由正弦定理可得2R=
=
=2
.
则b=2RsinB=2
sinB.
c=2RsinC=2
sin(
-B)=2
(sin
cosB-cos
sinB)=2
(
cosB+
sinB)=3cosB+
sinB.
三角形的周长为:a+b+c=3+2
sinB+3cosB+
sinB=3+3
sinB+3cosB=3+6sin(B+
).
| BC |
| sinA |
| 3 | ||||
|
| 3 |
则b=2RsinB=2
| 3 |
c=2RsinC=2
| 3 |
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
三角形的周长为:a+b+c=3+2
| 3 |
| 3 |
| 3 |
| π |
| 6 |
点评:本题考查正弦定理的应用,三角形中的几何计算,两角和与差的三角函数,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x、y满足约束条件
,则z=2x+4y+5的最小值为( )
|
| A、-10 | B、-15 |
| C、-20 | D、-25 |
已知
=(1,0,2),
=(0,1,3),则
=( )
| OA |
| OB |
| AB |
| A、(1,1,5) |
| B、(1,-1,-1) |
| C、(-1,1,1) |
| D、(1,-1,1,) |
函数y=log2x(2<x≤16)的值域是( )
| A、(1,4) |
| B、(1,4] |
| C、(0,∞) |
| D、(-∞,+∞) |
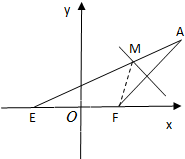 如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.
如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.