题目内容
f(x)是定义在D上的函数,若存在区间[m,n]⊆D,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x) 是k型函数.给出下列说法:①f(x)=3-
不可能是k型函数;
②若函数y=-
x2+x是3型函数,则m=-4,n=0;
③设函数f(x)=x3+2x2+x(x≤0)是k型函数,则k的最小值为
;
④若函数y=
(a≠0)是1型函数,则n-m的最大值为
.
下列选项正确的是( )
| 4 |
| x |
②若函数y=-
| 1 |
| 2 |
③设函数f(x)=x3+2x2+x(x≤0)是k型函数,则k的最小值为
| 4 |
| 9 |
④若函数y=
| (a2+a)x-1 |
| a2x |
2
| ||
| 3 |
下列选项正确的是( )
| A、①③ | B、②③ | C、②④ | D、①④ |
考点:命题的真假判断与应用,函数的值域
专题:简易逻辑
分析:根据题目中的新定义,结合函数与方程的知识,逐一判定命题①②③④是否正确,从而确定正确的答案.
解答:
解:对于①,f(x)的定义域是{x|x≠0},且f(2)=3-
=1,f(4)=3-
=2,
∴f(x)在[2,4]上的值域是[1,2],f(x)是
型函数,
∴①错误;
对于②,y=-
x2+x是3型函数,即-
x2+x=3x,解得x=0,或x=-4,∴m=-4,n=0,
∴②正确;
对于③,f(x)=x3+2x2+x(x≤0)是k型函数,则x3+2x2+x=kx有二不等负实数根,
即x2+2x+(1-k)=0有二不等负实数根,
∴
,解得0<k<1,
∴③错误;
对于④,y=
(a≠0)是1型函数,即(a2+a)x-1=a2x2,∴a2x2-(a2+a)x+1=0,
∴方程的两根之差x1-x2=
=
=
=
≤
,即n-m的最大值为
,∴④正确.
综上,正确的命题是②④.
故选:C.
| 4 |
| 2 |
| 4 |
| 4 |
∴f(x)在[2,4]上的值域是[1,2],f(x)是
| 1 |
| 2 |
∴①错误;
对于②,y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴②正确;
对于③,f(x)=x3+2x2+x(x≤0)是k型函数,则x3+2x2+x=kx有二不等负实数根,
即x2+2x+(1-k)=0有二不等负实数根,
∴
|
∴③错误;
对于④,y=
| (a2+a)x-1 |
| a2x |
∴方程的两根之差x1-x2=
| (x1+x2)2-4x1x2 |
(
|
1+
|
=
1+
|
2
| ||
| 3 |
2
| ||
| 3 |
综上,正确的命题是②④.
故选:C.
点评:本题是新定义题,考查了命题的真假判断与应用,考查了在新定义下函数的定义域、值域问题以及解方程的问题,是中档题也是易错题.

练习册系列答案
相关题目
已知实数x,y满足
,则2x+3y的最小值为( )
|
| A、7 | B、8 | C、9 | D、10 |
函数y=log2x(2<x≤16)的值域是( )
| A、(1,4) |
| B、(1,4] |
| C、(0,∞) |
| D、(-∞,+∞) |
已知双曲线C:
-
=1的点到焦点的最短距离为2,点P(3,4)在双曲线C的渐近线上,则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
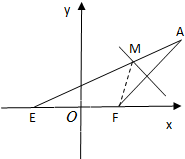 如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.
如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.