题目内容
(几何证明选讲选做题)已知PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于点B,PB=1,则AB= .
考点:与圆有关的比例线段
专题:推理和证明
分析:利用切割线定理,求出圆的半径,通过直角三角形求解cos∠AOB,然后利用余弦定理求解AB即可.
解答:
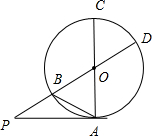 解:由题意可知图形如图:PA是圆O的切线,切点为A,可得AC⊥PA,
解:由题意可知图形如图:PA是圆O的切线,切点为A,可得AC⊥PA,
PA=2.AC是圆O的直径,PC与圆O交于点B,PB=1,
延长PO交圆与D,
由切割线定理可知:PA2=PB•PD,设圆的半径为r,
则:4=1(2r+1),解得r=
.
可得OB=OA=OD=
,cos∠AOB=
=
=
.
由余弦定理可得:AB2=OA2+OB2-2•OA•OBcos∠AOB=(
)2+(
)2-2×(
)2×
=
.
∴AB=
.
故答案为:
.
 解:由题意可知图形如图:PA是圆O的切线,切点为A,可得AC⊥PA,
解:由题意可知图形如图:PA是圆O的切线,切点为A,可得AC⊥PA,PA=2.AC是圆O的直径,PC与圆O交于点B,PB=1,
延长PO交圆与D,
由切割线定理可知:PA2=PB•PD,设圆的半径为r,
则:4=1(2r+1),解得r=
| 3 |
| 2 |
可得OB=OA=OD=
| 3 |
| 2 |
| OA |
| OP |
| ||
|
| 3 |
| 5 |
由余弦定理可得:AB2=OA2+OB2-2•OA•OBcos∠AOB=(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
| 5 |
∴AB=
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |
点评:本题考查直线与圆的位置关系,切割线定理的应用,余弦定理的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)满足2f(x)+f(-x)=3x+2,则f(2)=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若双曲线的标准方程为
-y2=1,则其渐近线方程是( )
| x2 |
| 4 |
| A、y=±4x | ||
B、y=±
| ||
| C、y=±2x | ||
D、y=±
|
已知
=(1,0,2),
=(0,1,3),则
=( )
| OA |
| OB |
| AB |
| A、(1,1,5) |
| B、(1,-1,-1) |
| C、(-1,1,1) |
| D、(1,-1,1,) |
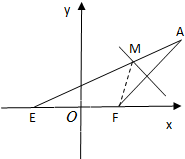 如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.
如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.