题目内容
双曲线
-
=1的焦距是 ．
| x2 |
| m2+12 |
| y2 |
| 4-m2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：首先判断双曲线的焦点在x轴上，求出a2，b2，由c2=a2+b2，计算可得c，即可得到焦距2c．
解答：
解：双曲线
-
=1焦点在x轴上，
即有4-m2＞0，
则a2=m2+12，b2=4-m2，
c2=a2+b2=16，
则c=4，焦距2c=8．
故答案为：8．
| x2 |
| m2+12 |
| y2 |
| 4-m2 |
即有4-m2＞0，
则a2=m2+12，b2=4-m2，
c2=a2+b2=16，
则c=4，焦距2c=8．
故答案为：8．
点评：本题考查双曲线的方程和性质，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知x、y满足约束条件
，则z=2x+4y+5的最小值为（ ）
|
| A、-10 | B、-15 |
| C、-20 | D、-25 |
直线x+y-2=0和7x-y+4=0所成的四个角的平分线方程是（ ）
| A、x-3y-7=0或6x+2y-3=0 |
| B、x+3y+7=0或6x+2y-3=0 |
| C、x-3y+7=0或6x+2y-3=0 |
| D、以上都不对 |
若双曲线的标准方程为
-y2=1，则其渐近线方程是（ ）
| x2 |
| 4 |
| A、y=±4x | ||
B、y=±
| ||
| C、y=±2x | ||
D、y=±
|
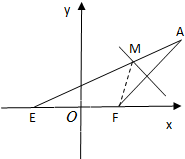如图，已知定点E（-1，0），F（1，0），动点A满足|AE|=4，线段AF的垂直平分线交AE于点M．