题目内容
已知数列{an}的前n项和为Sn,a1+a2=16且Sn=n+4+2Sn-1.
(1)求数列的通项公式an;
(2)若数列{bn}满足bn=nan,其前n项和为Tn,证明:存在唯一的n≠1,使得Tn=22n-17成立.
(1)求数列的通项公式an;
(2)若数列{bn}满足bn=nan,其前n项和为Tn,证明:存在唯一的n≠1,使得Tn=22n-17成立.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知求得数列首项,且得到an+1-an=an+1,由此构造出等比数列{an+1},求其通项公式即可得到数列的通项公式an;
(2)由bn=nan,利用错位相减法求得数列{bn}的前n项和为Tn,结合Tn=22n-17,由数列的函数特性借助于导数可证存在唯一的n≠1,使得Tn=22n-17成立.
(2)由bn=nan,利用错位相减法求得数列{bn}的前n项和为Tn,结合Tn=22n-17,由数列的函数特性借助于导数可证存在唯一的n≠1,使得Tn=22n-17成立.
解答:
(1)解:由Sn=n+4+2Sn-1,得an=n+4+Sn-1 ①,
则an+1=n+1+4+Sn ②,
②-①得:an+1-an=an+1,即an+1+1=2(an+1).
在Sn=n+4+2Sn-1中,取n=2,得a1+a2=6+2a1,
联立
,解得a1=5.
∴数列{an+1}是以a1+1=6为首项,以2为公比的等比数列,
∴an+1=6•2n-1,
an=6•2n-1-1=3•2n-1;
(2)证明:bn=nan=n(3×2ⁿ-1)=3×(n×2ⁿ)-n,
Tn=b1+b2+…+bn
=3×(1×2+2×22+3×23+…+n×2ⁿ)-(1+2+…+n)
=3×(1×2+2×22+3×23+…+n×2ⁿ)-
.
令Cn=1×2+2×22+3×23+…+n×2ⁿ,
则2Cn=1×22+2×23+…+(n-1)×2ⁿ+n×2n+1.
两式作差得-Cn=2+22+…+2ⁿ-n×2n+1=
-n×2n+1
=(1-n)×2n+1-2.
∴Cn=(n-1)×2n+1+2.
则Tn=3(n-1)×2n+1+6-
.
由Tn=22n-17,得3(n-1)×2n+1+6-
=22n-17.
即2n+1=
(n+46).
令f(n)=2n+1-
(n+46),
f′(n)=(n+1)ln2-
>0,
∴f(n)为递增数列,又f(2)=0.
∴存在唯一的n=2≠1,使得Tn=22n-17成立.
则an+1=n+1+4+Sn ②,
②-①得:an+1-an=an+1,即an+1+1=2(an+1).
在Sn=n+4+2Sn-1中,取n=2,得a1+a2=6+2a1,
联立
|
∴数列{an+1}是以a1+1=6为首项,以2为公比的等比数列,
∴an+1=6•2n-1,
an=6•2n-1-1=3•2n-1;
(2)证明:bn=nan=n(3×2ⁿ-1)=3×(n×2ⁿ)-n,
Tn=b1+b2+…+bn
=3×(1×2+2×22+3×23+…+n×2ⁿ)-(1+2+…+n)
=3×(1×2+2×22+3×23+…+n×2ⁿ)-
| n(n+1) |
| 2 |
令Cn=1×2+2×22+3×23+…+n×2ⁿ,
则2Cn=1×22+2×23+…+(n-1)×2ⁿ+n×2n+1.
两式作差得-Cn=2+22+…+2ⁿ-n×2n+1=
| 2(1-2n) |
| 1-2 |
=(1-n)×2n+1-2.
∴Cn=(n-1)×2n+1+2.
则Tn=3(n-1)×2n+1+6-
| n(n+1) |
| 2 |
由Tn=22n-17,得3(n-1)×2n+1+6-
| n(n+1) |
| 2 |
即2n+1=
| 1 |
| 6 |
令f(n)=2n+1-
| 1 |
| 6 |
f′(n)=(n+1)ln2-
| 1 |
| 6 |
∴f(n)为递增数列,又f(2)=0.
∴存在唯一的n=2≠1,使得Tn=22n-17成立.
点评:本题考查了数列递推式,考查了构造法求数列的通项公式,考查了数列的函数特性,训练了利用导数研究函数的单调性,是中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
直线x+y-2=0和7x-y+4=0所成的四个角的平分线方程是( )
| A、x-3y-7=0或6x+2y-3=0 |
| B、x+3y+7=0或6x+2y-3=0 |
| C、x-3y+7=0或6x+2y-3=0 |
| D、以上都不对 |
已知
=(1,0,2),
=(0,1,3),则
=( )
| OA |
| OB |
| AB |
| A、(1,1,5) |
| B、(1,-1,-1) |
| C、(-1,1,1) |
| D、(1,-1,1,) |
已知双曲线C:
-
=1的点到焦点的最短距离为2,点P(3,4)在双曲线C的渐近线上,则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
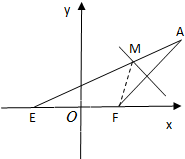 如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.
如图,已知定点E(-1,0),F(1,0),动点A满足|AE|=4,线段AF的垂直平分线交AE于点M.