题目内容
20.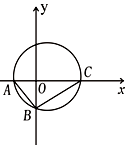 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.(1)求Rt△ABC外接圆的方程;
(2)求过点(0,3)且与Rt△ABC外接圆相切的直线的方程.
分析 (1)求出圆心为(1,0),半径为3,即可求Rt△ABC外接圆的方程;
(2)设所求直线方程为y=kx+3,即kx-y+3=0,当圆与直线相切时,有$d=\frac{{|{k+3}|}}{{\sqrt{{k^2}+1}}}=3$,即可求过点(0,3)且与Rt△ABC外接圆相切的直线的方程.
解答 解:(1)由题意可知点C在x轴的正半轴上,可设其坐标为(a,0),
又AB⊥BC,则kAB•kBC=-1,…(3分)
即$\frac{{-2\sqrt{2}}}{2}•\frac{{2\sqrt{2}}}{a}=-1$,解得a=4.…(6分)
则所求圆的圆心为(1,0),半径为3,故所求圆的方程为(x-1)2+y2=9.…(9分)
(2)由题意知直线的斜率存在,
故设所求直线方程为y=kx+3,即kx-y+3=0.…(12分)
当圆与直线相切时,有$d=\frac{{|{k+3}|}}{{\sqrt{{k^2}+1}}}=3$,解得k=0,或$k=\frac{3}{4}$…(15分)
故所求直线方程为y=3或$y=\frac{3}{4}x+3$,即y-3=0或3x-4y+12=0.…(17分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.已知某几何体的三视图如图,则该几何体的体积是( )
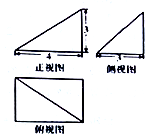

| A. | 48 | B. | 36 | C. | 24 | D. | 12 |
11.a>b的一个充分不必要条件是( )
| A. | a=1,b=0 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | a2>b2 | D. | a3>b3 |
15.圆x2+y2-6x-2y+3=0的圆心到直线x+ay-1=0的距离为1,则a=( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
5.方程log2x+x=3的解所在区间是( )
| A. | (0,1) | B. | (1,2) | C. | (3,+∞) | D. | [2,3) |
9.椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$中,以点M(1,2)为中点的弦所在直线斜率为( )
| A. | $\frac{9}{16}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{64}$ | D. | $-\frac{9}{32}$ |
10.已知集合A={x|x2-2x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A. | [-2,-1] | B. | [-1,2] | C. | [-1,1] | D. | [1,2] |