题目内容
5.方程log2x+x=3的解所在区间是( )| A. | (0,1) | B. | (1,2) | C. | (3,+∞) | D. | [2,3) |
分析 判断f(x)=log2x+x-3,在(0,+∞)上单调递增.根据函数的零点存在性定理得出答案.
解答 解:设f(x)=log2x+x-3,在(0,+∞)上单调递增.
∵f(2)=1+2-3=0,f(3)=log23>0
∴根据函数的零点存在性定理得出:f(x)的零点在[2,3]区间内
∴方程log2x+x=3的解所在的区间为[2,3],
故选:D.
点评 本题考查了函数的单调性,函数零点的判断,方程解所在的区间,属于中档题,但是难度不大,常规题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知函数$f(x)=\left\{{\begin{array}{l}{1-|x|,x≤1}\\{{{({x-1})}^2},x>1}\end{array}}\right.$,若方程f(1-x)-m=0有三个不相等的实数根,则实数m的取值范围为( )
| A. | (-∞,1) | B. | $({\frac{3}{4},+∞})$ | C. | (0,2) | D. | (0,1) |
16.等差数列{an}的前n项和为Sn,若a1009=1,则S2017( )
| A. | 1008 | B. | 1009 | C. | 2016 | D. | 2017 |
13.已知函数f(x)=x5+ax3+bx-8,且f(-2017)=10,则f(2017)等于( )
| A. | -26 | B. | -18 | C. | -10 | D. | 10 |
10.若函数f(x)=$\left\{\begin{array}{l}{{a}^{x},x≥1}\\{(4-\frac{a}{2})x+2,x<1}\end{array}\right.$且满足对任意的实数x1≠x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0成立,则实数a的取值范围是( )
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
14.对武汉市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如表:
(1)从这50人是否赞成“楼市限购政策”采取分层抽样,抽取一个容量为10的样本,问样本中赞成与不赞成“楼市限购政策”的人数各有多少名?
(2)根据以上统计数据填写下面2*2的列联表,并回答是否有95%的把握认为月收入以55百元为分界点对“楼市限购政策”的态度有差异?
(参考公式:${{K}^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 月收入(百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 8 | 12 | 4 | 2 | 1 |
(2)根据以上统计数据填写下面2*2的列联表,并回答是否有95%的把握认为月收入以55百元为分界点对“楼市限购政策”的态度有差异?
| 月收入低于55百元人数 | 月收入不低于55百元人数 | 合计 | |
| 赞成 | a=27 | b=3 | 30 |
| 不赞成 | c=13 | d=7 | 20 |
| 合计 | 40 | 10 | 40 |
| P( K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
15.定义在$(0\;,\;\frac{π}{2})$上的函数f(x),f'(x)是它的导函数,且恒有f(x)•tanx+f'(x)<0成立,则( )
| A. | $\sqrt{2}f(\frac{π}{3})>f(\frac{π}{4})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{6})$ | C. | $f(\frac{π}{3})>\sqrt{3}f(\frac{π}{6})$ | D. | $\sqrt{3}f(\frac{π}{3})<f(\frac{π}{6})$ |
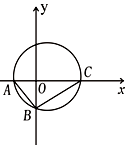 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.