题目内容
9.椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$中,以点M(1,2)为中点的弦所在直线斜率为( )| A. | $\frac{9}{16}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{64}$ | D. | $-\frac{9}{32}$ |
分析 先设出弦的两端点的坐标,分别代入椭圆方程,两式相减后整理即可求得弦所在的直线的斜率.
解答 解:设弦的两端点为A(x1,y1),B(x2,y2),
代入椭圆得$\left\{\begin{array}{l}\frac{{{x}_{1}}^{2}}{16}+\frac{{y}_{1}^{2}}{9}=1\\ \frac{{{x}_{2}}^{2}}{16}+\frac{{{y}_{2}}^{2}}{9}=1\end{array}\right.$,
两式相减得$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{16}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{9}$=0,
即$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{16}$=-$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{9}$,
即-$\frac{9({x}_{1}+{x}_{2})}{16({y}_{1}+{y}_{2})}$=$\frac{({y}_{1}-{y}_{2})}{({x}_{1}-{x}_{2})}$,
即-$\frac{9×2}{16×4}$=$\frac{({y}_{1}-{y}_{2})}{({x}_{1}-{x}_{2})}$,
即$\frac{({y}_{1}-{y}_{2})}{({x}_{1}-{x}_{2})}$=$-\frac{9}{32}$,
∴弦所在的直线的斜率为$-\frac{9}{32}$,
故选:D
点评 本题主要考查了椭圆的性质以及直线与椭圆的关系.在解决弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化,达到解决问题的目的.

| A. | $\sqrt{2}$或$\sqrt{5}$ | B. | 2或5 | C. | $\sqrt{5}$ | D. | 5 |
| 月收入(百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 8 | 12 | 4 | 2 | 1 |
(2)根据以上统计数据填写下面2*2的列联表,并回答是否有95%的把握认为月收入以55百元为分界点对“楼市限购政策”的态度有差异?
| 月收入低于55百元人数 | 月收入不低于55百元人数 | 合计 | |
| 赞成 | a=27 | b=3 | 30 |
| 不赞成 | c=13 | d=7 | 20 |
| 合计 | 40 | 10 | 40 |
| P( K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
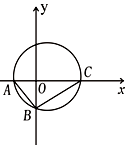 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.