题目内容
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、4 | ||
B、
| ||
| C、8 | ||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个以俯视图为底面的三棱锥，计算出底面面积和高，代入锥体体积公式，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个以俯视图为底面的三棱锥，
棱锥的底面面积S=
×2×2=2，
棱锥的高h=2，
故棱锥的体积V=
Sh=
，
故选：D
棱锥的底面面积S=
| 1 |
| 2 |
棱锥的高h=2，
故棱锥的体积V=
| 1 |
| 3 |
| 4 |
| 3 |
故选：D
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
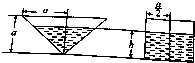一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图，两容器盛有液体的体积正好相等，且液面高均为h，求h．已知非空数集A、B、C，若A={y|y=x2，x∈B}，B={y|y=
，x∈C}，C={y|y=x3，x∈A}，则（ ）
| x |
| A、A=B=C |
| B、A=B≠C |
| C、A=C≠B |
| D、B=C≠A |