题目内容
1.若存在x∈(-1,1],使得不等式e2x-ax<a成立,则实数a的取值范围是( )| A. | $({-∞,\frac{2}{e}})$ | B. | ($\frac{2}{e}$,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | ($\frac{1}{e}$,+∞) |
分析 分类参数得a>$\frac{{e}^{2x}}{x+1}$,求出f(x)=$\frac{{e}^{2x}}{x+1}$在(-1,1]上的最小值即可得出a的范围.
解答 解:∵e2x-ax<a在(-1,1]上有解,∴a>$\frac{{e}^{2x}}{x+1}$在(-1,1]上有解,
令f(x)=$\frac{{e}^{2x}}{x+1}$,x∈(-1,1],则a>fmin(x).
则f′(x)=$\frac{{e}^{2x}(2x+1)}{(x+1)^{2}}$,
∴当x∈(-1,-$\frac{1}{2}$)时,f′(x)<0,当x∈(-$\frac{1}{2}$,1]时,f′(x)>0,
∴f(x)在(-1,-$\frac{1}{2}$]上单调递减,在(-$\frac{1}{2}$,1]上单调递增,
∴当x=-$\frac{1}{2}$时,f(x)取得最小值f(-$\frac{1}{2}$)=$\frac{2}{e}$.
∴a>$\frac{2}{e}$.
故选B.
点评 本题考查了函数的存在性问题与函数最值的计算,导数与函数单调性判断,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6.在△ABC中,a,b,c分别为内角A,B,C的对边,且a2=3b2+3c2-2$\sqrt{3}$bcsinA,则C的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
13.某校为了解学生对数学学案质量的满意度,从高一、高二两个年级分别随机调查了20个学生,得到对学案满意度评分(满分100分)的茎叶图如图:则下列说法错误的是( )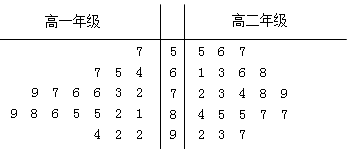

| A. | 高一学生满意度评分的平均值比高二学生满意度评分的平均值高 | |
| B. | 高一学生满意度评分比较集中,高二学生满意度评分比较分散 | |
| C. | 高一学生满意度评分的中位数为80 | |
| D. | 高二学生满意度评分的中位数为74 |
10.有5本相同的数学书和3本相同的语文书,要将它们排在同一层书架上,并且语文书不能放在一起,则不同的放法数为( )
| A. | 20 | B. | 120 | C. | 2400 | D. | 14400 |