��Ŀ����
16����֪$\overrightarrow{m}$=��$\sqrt{3}$sin$\frac{x}{3}$��cos$\frac{x}{3}$����$\overrightarrow{n}$=��cos$\frac{x}{3}$��cos$\frac{x}{3}$����f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$��������f��x������С�����ںͶԳ����ģ�
������a��b��c�ֱ��ǡ�ABC�ڽ�A��B��C���Եıߣ���a=2����2a-b��cosC=ccosB��f��A��=$\frac{3}{2}$����c��
���� ��������֪����ƽ������������������ɵ�f��x��=sin��$\frac{2x}{3}$+$\frac{��}{6}$��+$\frac{1}{2}$���������ڹ�ʽ������С�����ڣ���$\frac{2x}{3}$+$\frac{��}{6}$=k�У�k��Z�����ɽ��f��x���ĶԳ����ģ�
���������Ǻ͵����Һ�����ʽ���������ڽǺͶ���������֪�ȵȿɵ�2sinAcosC=sinA�����sinA��0������cosC=$\frac{1}{2}$���ɵ�C��ֵ����f��A��=sin��$\frac{2A}{3}$+$\frac{��}{6}$��+$\frac{1}{2}$=$\frac{3}{2}$���������A��ֵ���������Ҷ�������c��ֵ��
��� �⣺����f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$=$\sqrt{3}$sin$\frac{x}{3}$cos$\frac{x}{3}$+cos2$\frac{x}{3}$=$\frac{\sqrt{3}}{2}$sin$\frac{2x}{3}$+$\frac{cos\frac{2x}{3}+1}{2}$=sin��$\frac{2x}{3}$+$\frac{��}{6}$��+$\frac{1}{2}$��
��f��x������С������ΪT=$\frac{2��}{\frac{2}{3}}$=3�У�
����$\frac{2x}{3}$+$\frac{��}{6}$=k�У�k��Z����ã�x=-$\frac{��}{4}$+$\frac{3}{2}$k�У�k��Z��
��f��x���ĶԳ�����Ϊ����x=-$\frac{��}{4}$+$\frac{3}{2}$k�У�$\frac{1}{2}$��k��Z��
����a=2����2a-b��cosC=ccosB��
��2sinAcosC=sinCcosB+sinBcosC=sinA��
��sinA��0��
��cosC=$\frac{1}{2}$���ɵ�C=$\frac{��}{3}$��
�֡�f��A��=sin��$\frac{2A}{3}$+$\frac{��}{6}$��+$\frac{1}{2}$=$\frac{3}{2}$��
��sin��$\frac{2A}{3}$+$\frac{��}{6}$��=1��
��A=$\frac{��}{2}$��
��a=2��
��c=$\frac{a•sinC}{sinA}$=$\sqrt{3}$��
���� ������Ҫ������ƽ�����������������㣬���ڹ�ʽ�����Ǻ͵����Һ�����ʽ���������ڽǺͶ��������Ҷ����Լ����Һ�����ͼ������ʵ��ۺ�Ӧ�ã�������ת��˼�룬���ڻ����⣮

| A�� | $\frac{\sqrt{6}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{6}}{3}$ |
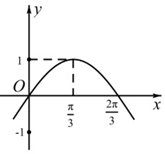 ��֪����f��x��=Asin����x+$\frac{��}{6}$��-1��A��0���أ�0���IJ���ͼ����ͼ�����������[0����]�ڵ�����ʵ��x1��x2��f��x1��-f��x2�������ֵΪ��������
��֪����f��x��=Asin����x+$\frac{��}{6}$��-1��A��0���أ�0���IJ���ͼ����ͼ�����������[0����]�ڵ�����ʵ��x1��x2��f��x1��-f��x2�������ֵΪ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 6 |
| A�� | $��{-�ޣ�\frac{2}{e}}��$ | B�� | ��$\frac{2}{e}$��+�ޣ� | C�� | $��{-�ޣ�\frac{1}{e}}��$ | D�� | ��$\frac{1}{e}$��+�ޣ� |
 ��ͼ��ʾ��������ABC-A1B1C1�ĵ����DZ߳�Ϊ2�������Σ�D��A1C1���е㣬��AA1��ƽ��ABC��AA1=3��
��ͼ��ʾ��������ABC-A1B1C1�ĵ����DZ߳�Ϊ2�������Σ�D��A1C1���е㣬��AA1��ƽ��ABC��AA1=3��