题目内容
12.数列{an}中,a2n=a2n-1+(-1)n,a2n+1=a2n+n,a1=1则a100=1226.分析 利用数列的递推关系式,推出偶数项的关系,然后求解即可.
解答 解:数列{an}中,a2n=a2n-1+(-1)n,a1=1,
则a2=1-1=0,a2n=a2n-1+(-1)n,可得:a2n+2=a2n+1+(-1)n+1,a2n+1=a2n+n,
可得a2n+2=a2n+n+(-1)n+1,
a4=a2+1+(-1)1+1,
a6=a4+2+(-1)2+1,
a8=a6+3+(-1)3+1,
…
a100=a98+49+(-1)49+1,
可得a100=0+1+2+3+…+49+1-1+1-1+…+1
=$\frac{49×50}{2}+1$=1226.
故答案为:1226.
点评 本题考查数列的递推关系式的应用,考查数列求和,是中档题.

练习册系列答案
相关题目
3.以点(2,-1)为圆心且与直线3x-4y+5=0相切的圆的方程为( )
| A. | (x-2)2+(y+1)2=3 | B. | (x+2)2+(y-1)2=3 | C. | (x-2)2+(y+1)2=9 | D. | (x+2)2+(y-1)2=9 |
7.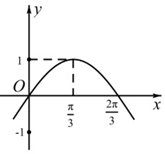 已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )
已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )
 已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )
已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
17.设直角坐标系xoy平面内的三点A(1,-2),B(a,-1),C(-b,0).其中a>0,b>0.若A,B,C三点共线.则$\frac{1}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
1.若存在x∈(-1,1],使得不等式e2x-ax<a成立,则实数a的取值范围是( )
| A. | $({-∞,\frac{2}{e}})$ | B. | ($\frac{2}{e}$,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | ($\frac{1}{e}$,+∞) |
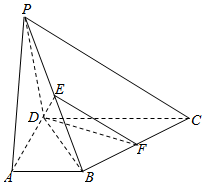 在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.
在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点. 如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.