题目内容
9.设△ABC的内角A、B、C所对的边分别为a、b、c且acosC-$\frac{1}{2}$c=b.若$a=2\sqrt{3}$则△ABC面积的最大值为$\sqrt{3}$.分析 acosC-$\frac{1}{2}$c=b.由余弦定理可得$a×\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$-$\frac{1}{2}$c=b,化为:b2+c2-a2=-bc.再利用余弦定理可得A.由b2+c2-a2=-bc.可得-$bc≥2bc-(2\sqrt{3})^{2}$,可得bc≤4.即可得出△ABC面积的最大值.
解答 解:∵acosC-$\frac{1}{2}$c=b.∴$a×\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$-$\frac{1}{2}$c=b,化为:b2+c2-a2=-bc.
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$,A∈(0,π).
∴A=$\frac{2π}{3}$.
∵b2+c2-a2=-bc.$a=2\sqrt{3}$.
∴-bc≥2bc-a2,可得bc≤4.
则△ABC面积S=$\frac{1}{2}bcsinA$$≤\frac{1}{2}×4×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了余弦定理、和差公式、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
19.数列{an}中,若存在ak,使得“ak>ak-1且ak>ak+1”成立(其中k≥2,k∈N*),ak则称为{an}的一个H值.现有如下数列:
①an=1-2n
②an=sinn
③an=$\frac{n-2}{{e}^{n-3}}$
④an=lnn-n
则存在H值的数列的序号为( )
①an=1-2n
②an=sinn
③an=$\frac{n-2}{{e}^{n-3}}$
④an=lnn-n
则存在H值的数列的序号为( )
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
17.设直角坐标系xoy平面内的三点A(1,-2),B(a,-1),C(-b,0).其中a>0,b>0.若A,B,C三点共线.则$\frac{1}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
14.已知某产品的广告费x(单位:万元)与销售额y(单位:万元)具有线性相关关系,其统计数据如下表:
由上表可得线性回归方程y=$\widehat{b}$x+a,据此模型预报广告费用为8万元时的销售额是( )
| X | 3 | 4 | 5 | 6 |
| Y | 25 | 30 | 40 | 45 |
| A. | 59.5 | B. | 52.5 | C. | 56 | D. | 63.5 |
1.若存在x∈(-1,1],使得不等式e2x-ax<a成立,则实数a的取值范围是( )
| A. | $({-∞,\frac{2}{e}})$ | B. | ($\frac{2}{e}$,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | ($\frac{1}{e}$,+∞) |
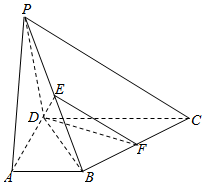 在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.
在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点. 如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
如图所示,三棱柱ABC-A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.