题目内容
设sin2α=-sinα,α∈(
,π),则tan2α的值是( )
| π |
| 2 |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
考点:二倍角的正弦
专题:计算题,三角函数的求值
分析:已知等式左边利用二倍角的正弦函数公式化简,根据sinα不为0求出cosα的值,由α的范围,利用同角三角函数间的基本关系求出sinα的值,进而求出tanα的值,所求式子利用二倍角的正切函数公式化简后,将tanα的值代入计算即可求出值.
解答:
解:∵sin2α=2sinαcosα=-sinα,α∈(
,π),
∴cosα=-
,sinα=
=
,
∴tanα=-
,
则tan2α=
=
.
故选:A.
| π |
| 2 |
∴cosα=-
| 1 |
| 2 |
| 1-cos2α |
| ||
| 2 |
∴tanα=-
| 3 |
则tan2α=
| 2tanα |
| 1-tan2α |
| 3 |
故选:A.
点评:此题考查了二倍角的正弦、正切函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
直线2x-my+1-3m=0,当m变动时,所有直线都通过定点( )
A、(-
| ||
B、(
| ||
C、(
| ||
D、(-
|
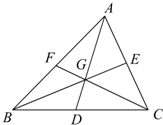 在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )
在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
函数f(x)=lgx+x-3的零点所在的区间是( )
| A、(1,2) |
| B、(3,4) |
| C、(2,3) |
| D、(0,1) |