题目内容
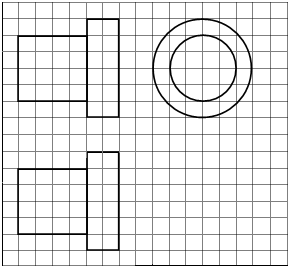 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图判断几何体的形状,通过三视图的数据求解几何体的体积即可.
解答:
解:几何体是由两个圆柱组成,一个是底面半径为3高为2,一个是底面半径为2,高为4,
组合体体积是:32π•2+22π•4=34π.
底面半径为3cm,高为6cm的圆柱体毛坯的体积为:32π×6=54π
切削掉部分的体积与原来毛坯体积的比值为:
=
.
故选:C.
组合体体积是:32π•2+22π•4=34π.

底面半径为3cm,高为6cm的圆柱体毛坯的体积为:32π×6=54π
切削掉部分的体积与原来毛坯体积的比值为:
| 54π-34π |
| 54π |
| 10 |
| 27 |
故选:C.
点评:本题考查三视图与几何体的关系,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
设函数f(x)=
sin
,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2,则m的取值范围是( )
| 3 |
| πx |
| m |
| A、(-∞,-6)∪(6,+∞) |
| B、(-∞,-4)∪(4,+∞) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-1)∪(1,+∞) |
设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩(∁RB)=( )
| A、(-3,0) |
| B、(-3,-1) |
| C、(-3,-1] |
| D、(-3,3) |
若实数k满足0<k<5,则曲线
-
=1与
-
=1的( )
| x2 |
| 16 |
| y2 |
| 5-k |
| x2 |
| 16-k |
| y2 |
| 5 |
| A、实半轴长相等 |
| B、虚半轴长相等 |
| C、离心率相等 |
| D、焦距相等 |
若变量x,y满足约束条件
,则z=2x+y的最大值等于( )
|
| A、7 | B、8 | C、10 | D、11 |
对任意等比数列{an},下列说法一定正确的是( )
| A、a1,a3,a9成等比数列 |
| B、a2,a3,a6成等比数列 |
| C、a2,a4,a8成等比数列 |
| D、a3,a6,a9成等比数列 |
若tanα>0,则( )
| A、sinα>0 |
| B、cosα>0 |
| C、sin2α>0 |
| D、cos2α>0 |