题目内容
13.某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期 末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学 成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据完成下面2×2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
(3)若以样本的频率作为概率,现从乙校总体中任取3人(每次抽取看作是独立重复的),求优秀学生人数ξ的分布列和数学期望.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
分析 (1)根据条件知道从甲校和乙校各自抽取的人数,做出频率分布表中的未知数;
(2)根据所给的条件写出列联表,根据列联表做出观测值,把观测值同临界值进行比较,得到没有99%的把握认为认为学生数学成绩优秀与所在学校有关.
(3)由题意知ξ的可能取值为0,1,2,3,ξ服从ξ~B(3,$\frac{2}{5}$)的二项分布,由P(ξ=k)=${C}_{3}^{k}$($\frac{2}{5}$)k($\frac{3}{5}$)3-k,(k=0,1,2,3),分别求得其概率,由ξ数学期望E(ξ)=np=3×$\frac{2}{5}$=$\frac{6}{5}$,即可求得优秀学生人数ξ的数学期望$\frac{6}{5}$.
解答 解:(1)由分层抽样可知:甲校抽取:105×$\frac{1100}{2100}$=55人,乙校抽取105-55=50,
∴2+3+10+15+15+x+3+1=55,解得:x=6,
由1+2+9+8+10+10+y+3=50,解得:y=7,
(2)由表中数据完成2×2列联表:
| 甲校 | 乙校 | 总计 | |
| 优秀 | 10 | 20 | 30 |
| 非优秀 | 45 | 30 | 75 |
| 总计 | 55 | 50 | 105 |
∴没有99%的把握认为学生数学成绩优秀与所在学校有关;
(3)由题意知,乙校优秀的概率为$\frac{2}{5}$,优秀学生人数ξ可能取值为0,1,2,3.
又ξ~B(3,$\frac{2}{5}$),且P(ξ=k)=${C}_{3}^{k}$($\frac{2}{5}$)k($\frac{3}{5}$)3-k,(k=0,1,2,3)
∴分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
优秀学生人数ξ的数学期望$\frac{6}{5}$.
点评 本题主要考查离散型随机变量的期望与方差、独立性检验的应用,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
3.直线的斜率为-2且与圆x2+y2=5相切的直线方程是( )
| A. | 2x-y+5=0或2x-y-5=0 | B. | 2x+y+5=0或2x+y-5=0 | ||
| C. | $2x-y+\sqrt{5}=0$或$2x+y-\sqrt{5}=0$ | D. | $2x-y+\sqrt{5}=0$或$2x-y-\sqrt{5}=0$ |
4.函数y=cosx在x=1处的导数是( )
| A. | 0 | B. | -sin1 | C. | cos1 | D. | 1 |
8.设向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,则关于x的方程$\overrightarrow{a}$x2+$\overrightarrow{b}$x+$\overrightarrow{c}$=0的解的情况是( )
| A. | 至少有一个实数解 | B. | 至多只有一个实数解 | ||
| C. | 至多有两个实数解 | D. | 可能有无数个实数解 |
3.用半径为6的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积为( )
| A. | 9$\sqrt{3}$π | B. | 18π | C. | 6π | D. | 3$\sqrt{3}$π |
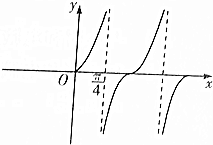 已知函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=tan(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.