题目内容
8.设向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,则关于x的方程$\overrightarrow{a}$x2+$\overrightarrow{b}$x+$\overrightarrow{c}$=0的解的情况是( )| A. | 至少有一个实数解 | B. | 至多只有一个实数解 | ||
| C. | 至多有两个实数解 | D. | 可能有无数个实数解 |
分析 向量a与b不共线,可设向量c=ma+nb,m,n均为实数,即a(x2+m)+b(x+n)=0.等价于求方程组x2+m=0,x+n=0的解即可判断.
解答 解:由题意:向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线,设向量$\overrightarrow{c}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$,m,n均为实数.
原方程可化为:$\overrightarrow{a}$x2+$\overrightarrow{b}$x+$\overrightarrow{c}$=0转化为$\overrightarrow{a}$x2+$\overrightarrow{b}$x+m$\overrightarrow{a}$+n$\overrightarrow{b}$=0,
即(m+x2)$\overrightarrow{a}$+(n+x)$\overrightarrow{b}$=0等价于求方程组m+x2=0,n+x=0的解.
该方程组可能一解,可能无解
则有一个解,否则无解
所以至多一个解.
故选B.
点评 本题主要考查平面向量的基本定理,即平面内任意向量都可由两不共线的非零向量唯一表示出来.

练习册系列答案
相关题目
18.设$f(x)=\left\{{\begin{array}{l}{{{log}_3}(x-8)(x≥9)}\\{f(x+6)(x<9)}\end{array}}\right.$,则f(5)的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
19.已知数列{an}的首项a1=1且an=-$\frac{1}{2}$an-1(n≥2),则a4等于( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{17}{24}$ | D. | -$\frac{1}{8}$ |
16.对于回归方程$\widehat{y}$=4.75x+257,当x=28时,y的估计值为( )
| A. | 390 | B. | 400 | C. | 420 | D. | 440 |
13.某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期 末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学 成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.
甲校:
乙校:
(1)求表中x与y的值;
(2)由以上统计数据完成下面2×2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
(3)若以样本的频率作为概率,现从乙校总体中任取3人(每次抽取看作是独立重复的),求优秀学生人数ξ的分布列和数学期望.
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据完成下面2×2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
(3)若以样本的频率作为概率,现从乙校总体中任取3人(每次抽取看作是独立重复的),求优秀学生人数ξ的分布列和数学期望.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
17.经过点A(-1,4),且斜率为-1的直线方程是( )
| A. | x+y+3=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x+y-5=0 |
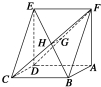 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.