题目内容

7．当x∈$[\frac{π}{6}，\frac{7π}{6}]$时，求函数y=3-sinx-2cos2x的最小值和最大值．

分析 利用三角函数的平方关系式，结合换元法，通过二次函数的闭区间的最值求解即可．

解答 解：y=3-sinx-2cos2x=3-sinx-2（1-sin2x）=2sin2x-sinx+1．…（3分）
令sin x=t，x∈$[\frac{π}{6}，\frac{7π}{6}]$，t∈[-$\frac{1}{2}$，1]，…（6分）
则原函数可化为y=2t2-t+1，t∈[-$\frac{1}{2}$，1]．…（8分）
当t=$\frac{1}{4}$时，ymin=$\frac{7}{8}$；  …（10分）
当t=-$\frac{1}{2}$或t=1时，ymax=2．…（12分）

点评 本题考查三角函数的化简，三角函数的最值的求法，保护费以及二次函数的最值的求法，考查计算能力．

练习册系列答案
相关题目
17．设幂函数f（x）=（a-1）xk（a∈R，k∈Q）的图象过点$（\sqrt{2}，2）$．
（1）求k，a的值；
（2）若函数h（x）=-f（x）+2b$\sqrt{f（x）}$+1-b在[0，2]上的最大值为3，求实数b的值．
18．已知命题p：$\frac{2x}{x-1}$＜1，命题q：（x+a）（x-3）＜0，若p是q的充分不必要条件，则实数a的取值范围是（　　）
A．（-3，-1]B．[-3，-1]C．[1，+∞）D．（-∞，-3]
15．已知直线y=kx+3与圆（x-2）2+（y-3）2=4相交于M，N两点，点$|MN|≥2\sqrt{3}$，求k的取值范围．
2．函数f（x）在[a，b]上有定义，若对任意x1，x2∈[a，b]，有f（$\frac{{x}_{1}+{x}_{2}}{2}$）≤$\frac{1}{2}$[f（x1）+f（x2）]，则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下题：
①f（x）在[1，3]上的图象时连续不断的  
②f（x）在[1，$\sqrt{3}$]上具有性质P
③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]
④对任意x1，x2，x3，x4∈[1，3]，有f（$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$）≤$\frac{1}{4}$[f（x1）+f（x2）+f（x3）+f（x4）]
其中真命题的序号③④．
12．已知函数$f（x）=sin（\frac{π}{6}-2x）$，x∈[0，π]，则f（x）的单调增区间为（　　）
A．$[0，\frac{π}{2}]$B．$[0，\frac{π}{3}]，[\frac{5π}{6}，π]$C．$[\frac{π}{3}，\frac{5π}{6}]$D．$[\frac{π}{2}，π]$
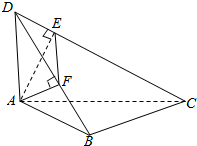19．已知a为常数，若曲线y=ax2+3x-lnx存在与直线x+y-1=0垂直的切线，则实数a的取值范围是[-$\frac{1}{2}$，+∞）．
16．已知x、y满足约束条$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$，则目标函数z=2x+y的最大值为10．
17．如图，在空间四边形ABCD中，DA⊥平面ABC，∠ABC=90°，AE⊥CD，AF⊥DB．
求证：（1）平面DBC⊥平面DAB；
（2）平面ADC⊥平面AEF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网