题目内容
17.设幂函数f(x)=(a-1)xk(a∈R,k∈Q)的图象过点$(\sqrt{2},2)$.(1)求k,a的值;
(2)若函数h(x)=-f(x)+2b$\sqrt{f(x)}$+1-b在[0,2]上的最大值为3,求实数b的值.
分析 (1)根据幂函数的定义和性质进行求解即可求k,a的值;
(2)若函数h(x)=-f(x)+2b$\sqrt{f(x)}$+1-b在[0,2]上的最大值为3,利用一元二次函数的性质即可求实数b的值.
解答 解:(1)设幂函数f(x)=(a-1)xk(a∈R,k∈Q)的图象过点$(\sqrt{2},2)$.
则a-1=1,即a=2,此时f(x)=xk,
即$(\sqrt{2})^{k}={2}^{\frac{k}{2}}$=2,即$\frac{k}{2}$=1,解得k=2;
(2)∵a=2,k=2,
∴f(x)=x2,
则h(x)=-f(x)+2b$\sqrt{f(x)}$+1-b=-x2+2bx+1-b
=-(x-b)2+1-b+b2,
若b<0,则函数h(x)在[0,2]上单调递减,最大值为h(0)=1-b=3,即b=-2,满足条件.
若0≤b≤2,此时当x=b时,最大值为h(b)=1-b+b2=3,
即b2-b-2=0,解得b=2或b=-1(舍).
若b>2,则函数h(x)在[0,2]上单调递增,最大值为h(2)=3b-3=3,即b=2,不满足条件
综上b=-2或b=2.
点评 本题主要考查幂函数的定义和性质的应用以及一元二次函数的性质,利用换元法结合一元二次函数的性质是解决本题的关键.注意要进行分类讨论.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.下列转化结果错误的是( )
| A. | 67°30′化成弧度是$\frac{3}{8}$π | B. | -$\frac{10}{3}$π化成度是-600° | ||
| C. | -150°化成弧度是$\frac{5}{6}$π | D. | $\frac{π}{12}$化成度是15° |
2.“(2x-1)x=0”是“x=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
6.命题“?x0∈R,3${\;}^{{x}_{0}}$+1≤$\frac{3}{2}$”的否定为( )
| A. | ?x0∈R,3${\;}^{{x}_{0}}$+1>$\frac{3}{2}$ | B. | ?x0∈R,3${\;}^{{x}_{0}}$+1≥$\frac{3}{2}$ | ||
| C. | ?x∈R,3x+1>$\frac{3}{2}$ | D. | ?x∈R,3x+1<$\frac{3}{2}$ |
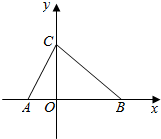 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$