题目内容
18.已知命题p:$\frac{2x}{x-1}$<1,命题q:(x+a)(x-3)<0,若p是q的充分不必要条件,则实数a的取值范围是( )| A. | (-3,-1] | B. | [-3,-1] | C. | [1,+∞) | D. | (-∞,-3] |
分析 解分式不等式求得命题P,解一元二次不等式求得命题q,再根据p是q的充分不必要条件,求得实数a的取值范围.
解答 解:命题p:$\frac{2x}{x-1}$<1,即:$\frac{x+1}{x-1}$<0,即 (x+1)(x-1)<0,即-1<x<1.
对于命题q:(x+a)(x-3)<0:当-a<3时,即-a<x<3;当-a>3时,即3<x<-a;当a=-3时,即∅.
若p是q的充分不必要条件,则有-a≤-1,求得a≥1,
故选:C.
点评 本题主要考查充分条件、必要条件、充要条件的定义,分式不等式的解法,属于基础题.

练习册系列答案
相关题目
6.命题“?x0∈R,3${\;}^{{x}_{0}}$+1≤$\frac{3}{2}$”的否定为( )
| A. | ?x0∈R,3${\;}^{{x}_{0}}$+1>$\frac{3}{2}$ | B. | ?x0∈R,3${\;}^{{x}_{0}}$+1≥$\frac{3}{2}$ | ||
| C. | ?x∈R,3x+1>$\frac{3}{2}$ | D. | ?x∈R,3x+1<$\frac{3}{2}$ |
13.若函数y=x2-x的图象在点x=2处的切线被圆C:x2+y2=r2(r>0)所截得的弦长是$\frac{2\sqrt{10}}{5}$,则r=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
3.下列各图中,不可能表示函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
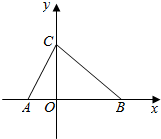 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$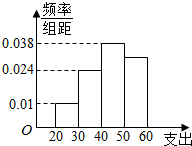 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )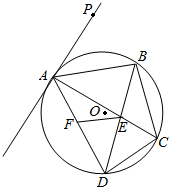 已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.
已知:如图,四边形ABCD是圆O的内接四边形,对角线AC、BD交于点E,直线AP是圆O的切线,切点为A,∠PAB=∠BAC.