题目内容
15.已知直线y=kx+3与圆(x-2)2+(y-3)2=4相交于M,N两点,点$|MN|≥2\sqrt{3}$,求k的取值范围.分析 利用垂径定理及勾股定理表示出弦长|MN|,列出关于k的不等式,求出不等式的解集即可得到k的范围.
解答 解:由圆的方程得:圆心(2,3),半径r=2,
∵圆心到直线y=kx+3的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$,|MN|≥2$\sqrt{3}$,
∴2$\sqrt{4-\frac{4{k}^{2}}{{k}^{2}+1}}$≥2$\sqrt{3}$,
变形整理得4k2+4-4k2≥3k2+3,
解得:-$\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$,
∴k的取值范围是[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$].
点评 本题考查了直线与圆相交的性质,考查垂径定理及勾股定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
5.下列转化结果错误的是( )
| A. | 67°30′化成弧度是$\frac{3}{8}$π | B. | -$\frac{10}{3}$π化成度是-600° | ||
| C. | -150°化成弧度是$\frac{5}{6}$π | D. | $\frac{π}{12}$化成度是15° |
6.命题“?x0∈R,3${\;}^{{x}_{0}}$+1≤$\frac{3}{2}$”的否定为( )
| A. | ?x0∈R,3${\;}^{{x}_{0}}$+1>$\frac{3}{2}$ | B. | ?x0∈R,3${\;}^{{x}_{0}}$+1≥$\frac{3}{2}$ | ||
| C. | ?x∈R,3x+1>$\frac{3}{2}$ | D. | ?x∈R,3x+1<$\frac{3}{2}$ |
3.下列各图中,不可能表示函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  |
10.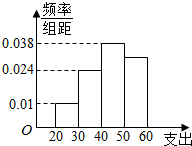 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有30人,则n的值为( )| A. | 100 | B. | 1000 | C. | 90 | D. | 900 |
20.若全集U=R,集合M={x|x2>4},N={x|$\frac{3-x}{x+1}$>0},则M∩(∁UN)等于( )
| A. | {x|x<-2} | B. | {x|x<-2}或x≥3} | C. | {x|x≥32} | D. | {x|-2≤x<3} |
4.方程${log_{\frac{1}{2}}}x={2^x}-2016$的实数根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |