题目内容
已知箱子中装有标号分别为1,2,3,4,5的五个小球.现从该箱子中取球,每次取一个球(无放回,且每球取到的机会均等).
(Ⅰ)若连续取两次,求取出的两球上标号都是奇数或都是偶数的概率;
(Ⅱ)若取出的球的标号为奇数即停止取球,否则继续取,求取出次数X的分布列和数学期望E(X).
(Ⅰ)若连续取两次,求取出的两球上标号都是奇数或都是偶数的概率;
(Ⅱ)若取出的球的标号为奇数即停止取球,否则继续取,求取出次数X的分布列和数学期望E(X).
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式
专题:概率与统计
分析:(Ⅰ)设事件A为“两球上的标号都是奇数或都是偶数”,利用古典概率计算公式能求出取出的两球上标号都是奇数或都是偶数的概率.
(Ⅱ)由题意得X=1,2,3,分别求出P(X=1),P(X=2),P(X=3由,由此能求出X的分布列和E(X).
(Ⅱ)由题意得X=1,2,3,分别求出P(X=1),P(X=2),P(X=3由,由此能求出X的分布列和E(X).
解答:
解:(Ⅰ)设事件A为“两球上的标号都是奇数或都是偶数”,
则P(A)=
=
.
∴取出的两球上标号都是奇数或都是偶数的概率为
.
(Ⅱ)由题意得X=1,2,3,
则P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
∴X的分布列为:
∴E(X)=1×
+2×
+3×
.
则P(A)=
| ||||||||
|
| 2 |
| 5 |
∴取出的两球上标号都是奇数或都是偶数的概率为
| 2 |
| 5 |
(Ⅱ)由题意得X=1,2,3,
则P(X=1)=
| ||
|
| 3 |
| 5 |
P(X=2)=
| ||||
|
| 3 |
| 10 |
P(X=3)=
| ||||||
|
| 1 |
| 10 |
∴X的分布列为:
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 3 |
| 5 |
| 3 |
| 10 |
| 1 |
| 10 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要注意排列组合的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合P={x|y=x2},Q={y|y=x2},则下列关系正确的是( )
| A、P?Q | B、P=Q |
| C、P⊆Q | D、P?Q |
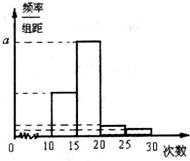 对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: