题目内容
在平面直角坐标系xOy中,已知椭圆C:
+
=1(a>b>0)与直线l:x=m(m∈R).四点(3,1),(3,-1),(-2
,0),(
,
)中有三个点在椭圆C上,剩余一个点在直线l上.
(1)求椭圆C的方程;
(2)若动点P在直线l上,过P作直线交椭圆C于M,N两点,使得PM=PN,再过P作直线l′⊥MN.证明:直线l′恒过定点,并求出该定点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 3 |
(1)求椭圆C的方程;
(2)若动点P在直线l上,过P作直线交椭圆C于M,N两点,使得PM=PN,再过P作直线l′⊥MN.证明:直线l′恒过定点,并求出该定点的坐标.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)判断点(3,1),(3,-1),点(
,
)在椭圆C上,点(-2
,0)在直线l上,代入椭圆方程,即可求出椭圆C的方程;
(2)分类讨论,利用点差法求出直线l′的方程,可得直线l′恒过定点.
| 3 |
| 3 |
| 2 |
(2)分类讨论,利用点差法求出直线l′的方程,可得直线l′恒过定点.
解答:
(1)解:由题意有3个点在椭圆C上,根据椭圆的对称性,则点(3,1),(3,-1)一定在椭圆C上,
即
+
=1 ①,…(2分)
若点(-2
,0)在椭圆C上,则点(-2
,0)必为C的左顶点,
而3>2
,则点(-2
,0)一定不在椭圆C上,
故点(
,
)在椭圆C上,点(-2
,0)在直线l上,…(4分)
所以
+
=1 ②,
联立①②可解得a2=12,b2=4,
所以椭圆C的方程为
+
=1; …(6分)
(2)证明:由(1)可得直线l的方程为x=-2
,设P(-2
,y0),y0∈(-
,
),
当y0≠0时,设 M(x1,y1)、N (x2,y2),显然x1≠x2,
联立
,则
+
=0,即
=-
•
,
又PM=PN,即P为线段MN的中点,
故直线MN的斜率为-
•
=
,…(10分)
又l′⊥MN,所以直线l′的方程为y-y0=-
(x+2
),…(13分)
即y═-
(x+
),
显然l′恒过定点(-
,0),…(15分)
当y0=0时,直线MN即x=-2
,此时l′为x轴亦过点(-
,0);
综上所述,l′恒过定点(-
,0). …(16分)
即
| 9 |
| a2 |
| 1 |
| b2 |
若点(-2
| 2 |
| 2 |
而3>2
| 2 |
| 2 |
故点(
| 3 |
| 3 |
| 2 |
所以
| 3 |
| a2 |
| 3 |
| b2 |
联立①②可解得a2=12,b2=4,
所以椭圆C的方程为
| x2 |
| 12 |
| y2 |
| 4 |
(2)证明:由(1)可得直线l的方程为x=-2
| 2 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
当y0≠0时,设 M(x1,y1)、N (x2,y2),显然x1≠x2,
联立
|
| x12-x22 |
| 12 |
| y12-y22 |
| 4 |
| y1-y2 |
| x1-x2 |
| 1 |
| 3 |
| x1+x2 |
| y1+y2 |
又PM=PN,即P为线段MN的中点,
故直线MN的斜率为-
| 1 |
| 3 |
-2
| ||
| y0 |
2
| ||
| 3y0 |
又l′⊥MN,所以直线l′的方程为y-y0=-
| 3y0 | ||
2
|
| 2 |
即y═-
| 3y0 | ||
2
|
4
| ||
| 3 |
显然l′恒过定点(-
4
| ||
| 3 |
当y0=0时,直线MN即x=-2
| 2 |
4
| ||
| 3 |
综上所述,l′恒过定点(-
4
| ||
| 3 |
点评:本题考查椭圆的标准方程,考查点差法的运用,考查分类讨论的数学思想,正确运用点差法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
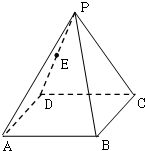 如图,在各棱长都相等且底面为正方形的四棱锥P-ABCD中,E为PD的中点.
如图,在各棱长都相等且底面为正方形的四棱锥P-ABCD中,E为PD的中点.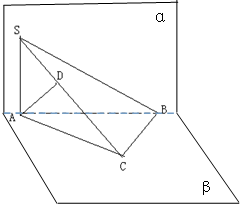 已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,
已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,