题目内容
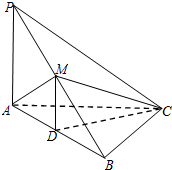 如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.
如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.(1)求证:BC⊥平面PAC;
(2)若BC=4,PB=10,求点B到平面DCM的距离.
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:(1)要证BC⊥平面PAC,只需证明BC与平面PAC内的两条相交直线PA、PC垂直,利用直线与平面垂直的判定定理证明即可;
(2)解法一:通过BC=4,PB=10,利用等体积法VM-BCD=VB-MCD,即可求解点B到平面DCM的距离.
解法二:过点B作直线CD的垂线,交CD的延长线于点H,证明BH⊥平面DCM.说明BH为点B到平面DCM的距离,一是利用等面积法求解,二是利用解直角三角形求解.
(2)解法一:通过BC=4,PB=10,利用等体积法VM-BCD=VB-MCD,即可求解点B到平面DCM的距离.
解法二:过点B作直线CD的垂线,交CD的延长线于点H,证明BH⊥平面DCM.说明BH为点B到平面DCM的距离,一是利用等面积法求解,二是利用解直角三角形求解.
解答:
 (本小题满分14分)
(本小题满分14分)
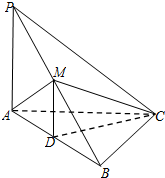
(1)证明:在正△AMB中,D是AB的中点,∴MD⊥AB.…(1分)
∵M是PB的中点,D是AB的中点,∴MD∥PA,故PA⊥AB.…(2分)
又PA⊥AC,AB∩AC=A,AB,AC?平面ABC,
∴PA⊥平面ABC.…(4分)
∵BC?平面ABC,∴PA⊥BC.…(5分)
又PC⊥BC,PA∩PC=P,PA,PC?平面PAC,
∴BC⊥平面PAC.…(7分)
(2)解法1:设点B到平面DCM的距离为h,…(8分)
∵PB=10,M是PB的中点,∴MB=5.
∵△AMB为正三角形,∴AB=MB=5.…(9分)
∵BC=4,BC⊥AC,∴AC=3.
∴S△BCD=
S△ABC=
×
×BC×AC=
×
×4×3=3.…(10分)
∵MD=
=
,
由(1)知MD∥PA,∴MD⊥DC.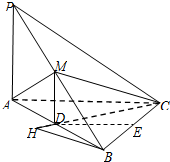
在△ABC中,CD=
AB=
,
∴S△MCD=
×MD×CD=
×
×
=
.…(11分)
∵VM-BCD=VB-MCD,…(12分)
∴
S△BCD•MD=
S△MCD•h,
即
×3×
=
×
×h.…(13分)
∴h=
.
故点B到平面DCM的距离为
.…(14分)
解法2:过点B作直线CD的垂线,交CD的延长线于点H,…(8分)
由(1)知,PA⊥平面ABC,MD∥PA,
∴MD⊥平面ABC.
∵BH?平面ABC,∴MD⊥BH.
∵CD∩MD=D,∴BH⊥平面DCM.
∴BH为点B到平面DCM的距离.…(9分)
∵PB=10,M是PB的中点,∴MB=5.
∵△AMB为正三角形,∴AB=MB=5.…(10分)
∵D为AB的中点,∴CD=BD=
.
以下给出两种求BH的方法:
方法1:在△BCD中,过点D作BC的垂线,垂足为点E,
则DE=
AC=
.…(11分)
∵
×CD×BH=
×BC×DE,…(12分)
∴BH=
=
=
.
方法2:在Rt△BHD中,BH2+DH2=BD2=
. ①…(11分)
在Rt△BHC中,∵BC=4,
∴BH2+CH2=BC2,
即BH2+(DH+
)2=16. ②…(12分)
由①,②解得BH=
.
故点B到平面DCM的距离为
.…(14分)
 (本小题满分14分)
(本小题满分14分)(1)证明:在正△AMB中,D是AB的中点,∴MD⊥AB.…(1分)
∵M是PB的中点,D是AB的中点,∴MD∥PA,故PA⊥AB.…(2分)
又PA⊥AC,AB∩AC=A,AB,AC?平面ABC,
∴PA⊥平面ABC.…(4分)
∵BC?平面ABC,∴PA⊥BC.…(5分)
又PC⊥BC,PA∩PC=P,PA,PC?平面PAC,
∴BC⊥平面PAC.…(7分)
(2)解法1:设点B到平面DCM的距离为h,…(8分)
∵PB=10,M是PB的中点,∴MB=5.
∵△AMB为正三角形,∴AB=MB=5.…(9分)
∵BC=4,BC⊥AC,∴AC=3.
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵MD=
52-(
|
5
| ||
| 2 |
由(1)知MD∥PA,∴MD⊥DC.

在△ABC中,CD=
| 1 |
| 2 |
| 5 |
| 2 |
∴S△MCD=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
| 5 |
| 2 |
25
| ||
| 8 |
∵VM-BCD=VB-MCD,…(12分)
∴
| 1 |
| 3 |
| 1 |
| 3 |
即
| 1 |
| 3 |
5
| ||
| 2 |
| 1 |
| 3 |
25
| ||
| 8 |
∴h=
| 12 |
| 5 |
故点B到平面DCM的距离为
| 12 |
| 5 |
解法2:过点B作直线CD的垂线,交CD的延长线于点H,…(8分)
由(1)知,PA⊥平面ABC,MD∥PA,
∴MD⊥平面ABC.
∵BH?平面ABC,∴MD⊥BH.
∵CD∩MD=D,∴BH⊥平面DCM.
∴BH为点B到平面DCM的距离.…(9分)
∵PB=10,M是PB的中点,∴MB=5.
∵△AMB为正三角形,∴AB=MB=5.…(10分)
∵D为AB的中点,∴CD=BD=
| 5 |
| 2 |
以下给出两种求BH的方法:
方法1:在△BCD中,过点D作BC的垂线,垂足为点E,
则DE=
| 1 |
| 2 |
| 3 |
| 2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BH=
| BC×DE |
| CD |
4×
| ||
|
| 12 |
| 5 |
方法2:在Rt△BHD中,BH2+DH2=BD2=
| 25 |
| 4 |
在Rt△BHC中,∵BC=4,
∴BH2+CH2=BC2,
即BH2+(DH+
| 5 |
| 2 |
由①,②解得BH=
| 12 |
| 5 |
故点B到平面DCM的距离为
| 12 |
| 5 |
点评:本题考查直线与平面垂直的判断与证明,点到平面的距离的求法,考查空间想象能力以及逻辑推理能力.

练习册系列答案
相关题目
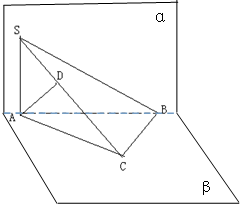 已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,
已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,