题目内容
已知椭圆C:
+y2=1(a>0)的一个焦点为(
,0).
(1)求a的值.
(2)直线l经过点P(
,
),且与椭圆C交于A、B两点,若点P恰为线段AB的中点,求直线l的方程.
| x2 |
| a2 |
| 3 |
(1)求a的值.
(2)直线l经过点P(
| 1 |
| 2 |
| 1 |
| 2 |
考点:直线与圆锥曲线的关系,直线的一般式方程,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆C:
+y2=1(a>0)的一个焦点为(
,0),可得a2-1=3,即可求出a;
(2)设A(x1,y1),B(x2,y2),则x1+x2=1,y1+y2=1,利用点差法求出直线的向量,可求直线l的方程.
| x2 |
| a2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),则x1+x2=1,y1+y2=1,利用点差法求出直线的向量,可求直线l的方程.
解答:
解:(1)∵椭圆C:
+y2=1(a>0)的一个焦点为(
,0),
∴a2-1=3,
∴a=2;
(2)设A(x1,y1),B(x2,y2),则x1+x2=1,y1+y2=1;
由(1)知,x12+4y12=4,①x22+4y22=4,②
①-②得:(x1+x2)(x1-x2)+4(y1+y2)(y2-y1)=0,
∴(x1-x2)+4(y2-y1)=0,
由题意知,直线l的斜率存在,k=
=-
,
∴直线l的方程为y-
=-
(x-
),即2x+8y-5=0.
| x2 |
| a2 |
| 3 |
∴a2-1=3,
∴a=2;
(2)设A(x1,y1),B(x2,y2),则x1+x2=1,y1+y2=1;
由(1)知,x12+4y12=4,①x22+4y22=4,②
①-②得:(x1+x2)(x1-x2)+4(y1+y2)(y2-y1)=0,
∴(x1-x2)+4(y2-y1)=0,
由题意知,直线l的斜率存在,k=
| y2-y1 |
| x2-x1 |
| 1 |
| 4 |
∴直线l的方程为y-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查椭圆的标准方程与几何性质,考查点差法求直线方程,正确运用点差法是关键.

练习册系列答案
相关题目

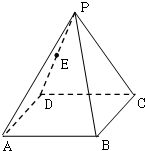 如图,在各棱长都相等且底面为正方形的四棱锥P-ABCD中,E为PD的中点.
如图,在各棱长都相等且底面为正方形的四棱锥P-ABCD中,E为PD的中点.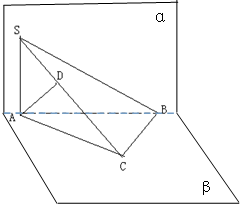 已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,
已知直二面角α-AB-β中,S∈平面α,C∈平面β,∠ACB=90°,SA⊥AB,AD⊥SC于D,