题目内容
2.若函数f(x)=($\frac{1}{2}$)x,g(x)=|log3(x-1)|,则方程f(x)-g(x)=0的实根个数为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 利用两个函数的图象判断交点个数即可.
解答 解:在同一个坐标系中画出两个函数f(x)=($\frac{1}{2}$)x,g(x)=|log3(x-1)|的图象,如图:
可知两个函数的图象有2个交点,
则方程f(x)-g(x)=0的实根个数为2.
故选:B.
点评 本题考查函数的图象的应用,零点个数的判断,考查数形结合思想的应用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
10.已知x,y是[0,1]上的两个随机数,则x,y满足y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
17.设等比数列{an}的公比为q,前n项和为Sn,则“q=1”是“S6=3S2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知cos(x-$\frac{π}{3}$)=$\frac{1}{3}$,则cos(2x-$\frac{5π}{3}$)+sin2($\frac{π}{3}$-x)的值为( )
| A. | -$\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
11.已知函数f(x)=|lnx|,$g(x)=\left\{\begin{array}{l}0,0<x≤1\\|{x^2}-4|-2,x>1\end{array}\right.$若方程|f(x)+g(x)|=a有4个实根,则a的取值范围是( )
| A. | (0,1] | B. | (0,2-ln2) | C. | [1,2-ln2] | D. | [1,2-ln2) |
12.角α的终边经过的一点P的坐标是(-$\sqrt{3}$,a),则“|a|=1”的充要条件是( )
| A. | $sinα=\frac{1}{2}$ | B. | $cosα=-\frac{{\sqrt{3}}}{2}$ | C. | $tanα=-\frac{{\sqrt{3}}}{3}$ | D. | $|PO|=\sqrt{3}+1$ |
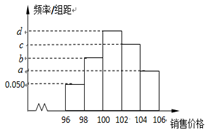 某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.
某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.