题目内容
17.设等比数列{an}的公比为q,前n项和为Sn,则“q=1”是“S6=3S2”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 S6=3S2,q=1时,6a1=3×2a1恒成立.q≠1时,$\frac{{a}_{1}({q}^{6}-1)}{q-1}$=$3×\frac{{a}_{1}({q}^{2}-1)}{q-1}$,解得q即可判断出结论.
解答 解:∵S6=3S2,∴q=1时,6a1=3×2a1恒成立.
q≠1时,$\frac{{a}_{1}({q}^{6}-1)}{q-1}$=$3×\frac{{a}_{1}({q}^{2}-1)}{q-1}$,
化为:q4+q2+1=3,即q4+q2-2=0,
解得q2=1,解得q=-1.
综上可得:“q=1”是“S6=3S2”的充分不必要条件.
故选:A.
点评 本题考查了等比数列的求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.f(x)=|x-2017|+|x-2016|+…+|x-1|+|x+1|+…+|x+2016|+|x+2017|,在不等式e2017x≥ax+1(x∈R)恒成立的条件下等式f(2018-a)=f(2017-b)恒成立,求b的取值集合( )
| A. | {b|2016≤b≤2018} | B. | {2016,2018} | C. | {2018} | D. | {2017} |
12.设全集U=R,集合A={y|y=x2-2},B={x|y=log2(3-x),则(∁UA)∩B=( )
| A. | {x|-2≤x<3} | B. | {x|x≤-2} | C. | {x|x<-2} | D. | {x|x<3} |
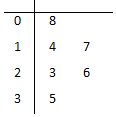 据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级.某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.