题目内容
12.(x+$\frac{2}{\sqrt{x}}$)6的展开式中,x3项的系数是60(用数字作答)分析 根据二项式展开式的通项公式,列方程求出r的值,
再求展开式中含x3项的系数.
解答 解:(x+$\frac{2}{\sqrt{x}}$)6的展开式中,
通项公式为
Tr+1=${C}_{6}^{r}$•x6-r•${(\frac{2}{\sqrt{x}})}^{r}$=${C}_{6}^{r}$•2r•${x}^{6-\frac{3r}{2}}$;
令6-$\frac{3r}{2}$=3,
解得r=2,
∴展开式中含x3项的系数是${C}_{6}^{2}$•22=60.
故答案为:60.
点评 本题考查了二项式展开式的通项公式应用问题,是基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.设集合A={x1,x2,x3,x4},xi∈{-1,0,1},i={1,2,3,4},那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为( )
| A. | 60 | B. | 65 | C. | 80 | D. | 81 |
20.若圆C1(x-m)2+(y-2n)2=m2+4n2+10(mn>0)始终平分圆C2:(x+1)2+(y+1)2=2的周长,则$\frac{1}{m}$+$\frac{2}{n}$的最小值为( )
| A. | $\frac{9}{2}$ | B. | 9 | C. | 6 | D. | 3 |
17.已知集合A={x|x2-3x-4≥0},B={x|2<x<5},则A∩B=( )
| A. | (1,5) | B. | [1,5) | C. | (4,5) | D. | [4,5) |
4.某化肥厂用三种原料生产甲乙两种肥料,生产1吨甲种肥料和生产1吨乙种肥料所需三种原料的吨数如右表所示:已知生产1吨甲种肥料产生的利润2万元,生产1吨乙种肥料产生的利润为3万元,现有A种原料20吨,B种原料36吨,C种原料32吨,在此基础上安排生产,则生产甲乙两种肥料的利润之和的最大值为( )
 | A | B | C |
| 甲 | 2 | 4 | 2 |
| 乙 | 4 | 4 | 8 |
| A. | 17万元 | B. | 18万元 | C. | 19万元 | D. | 20万元 |
1.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),过双曲线右焦点F倾斜角为$\frac{π}{4}$直线与该双曲线的渐近线分别交于M、N,O为坐标原点,若△OMF与△ONF的面积比等于2:1,则该双曲线的离心率等于( )
| A. | $\sqrt{3}$或$\frac{\sqrt{10}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{10}}{3}$或$\sqrt{10}$ | D. | $\frac{\sqrt{10}}{3}$ |
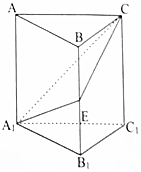 如图,在正三棱柱ABC-A1B1C1中,A1B1=2,AA1=h,E为BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,A1B1=2,AA1=h,E为BB1的中点.