Question

函数y=（

1

3

）^|x-1|+4cos²

π

2

x-2（-3≤x≤5），则此函数的所有零点之和等于

 

．

Answer 1

考点：函数零点的判定定理

专题：计算题,作图题,函数的性质及应用

分析：化简y=（

1

3

）^|x-1|+4cos²

π

2

x-2=（

1

3

）^|x-1|+2cos（πx）；从而得到其图象关于x=1对称，再化函数的零点个数即y=（

1

3

）^|x-1|与y=-2cos（πx）的交点的个数，从而求到个数，从而解得．

解答： 解：y=（

1

3

）^|x-1|+4cos²

π

2

x-2
=（

1

3

）^|x-1|+2cos（πx）；
其图象关于x=1对称，
此函数的零点个数即y=（

1

3

）^|x-1|与y=-2cos（πx）的交点的个数，
作y=（

1

3

）^|x-1|与y=-2cos（πx）的图象如下，

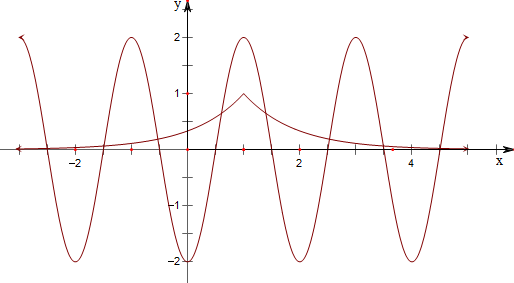
由图象可知，其共有8个零点，
又由其图象关于x=1对称知，
8个零点之和为8×1=8；
故答案为：8．

点评：本题考查了函数的零点与方程的根的关系，属于中档题．