题目内容
已知O是坐标原点，点A（-1，1），若点M（x，y）为平面区域
上的一个动点，则
•
的取值范围是（ ）
|
| AO |
| OM |
| A、[-2，0] |
| B、[-2，0） |
| C、[0，2] |
| D、（0，2] |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，设z=
•
，求出z的表达式，利用z的几何意义，利用数形结合即可得到结论．
| AO |
| OM |
解答：
解：不等式组等价为
，
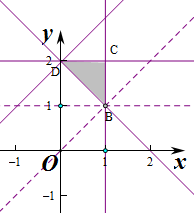
作出不等式组对应的平面区域如图：
设z=
•
，
∵A（-1，1），M（x，y），
∴z=
•
=x-y，
即y=x-z，
平移直线y=x-z，由图象可知当y=x-z，经过点D（0，2）时，直线截距最大，此时z最小为z=0-2=-2．
当直线y=x-z，经过点B（1，1）时，直线截距最小，此时z最大为z=1-1=0．
故-2≤z＜0，
故选：B．
|
作出不等式组对应的平面区域如图：
设z=
| AO |
| OM |
∵A（-1，1），M（x，y），
∴z=
| AO |
| OM |
即y=x-z，
平移直线y=x-z，由图象可知当y=x-z，经过点D（0，2）时，直线截距最大，此时z最小为z=0-2=-2．
当直线y=x-z，经过点B（1，1）时，直线截距最小，此时z最大为z=1-1=0．
故-2≤z＜0，
故选：B．
点评：本题主要考查线性规划的应用，根据向量数量积的坐标公式求出z的表达式，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
如果函数y=f（x）在区间I上是增函数，而函数y=
在区间I上是减函数，那么称函数y=f（x）是区间I上“缓增函数”，区间I叫做“缓增区间”，若函数f（x）=
x2-x+
是区间I上“缓增函数”，则“缓增区间”I为（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| A、[1，+∞） | ||
B、[0，
| ||
| C、[0，1] | ||
D、[1，
|
已知定义在R上的连续函数f（x）是一个奇函数，则
[ex+f（x）]dx等于（ ）
| ∫ | 1 -1 |
A、e+
| ||
B、e-
| ||
| C、0 | ||
| D、无法计算 |
函数y=3cos（
x-
）的最小正周期是（ ）
| 2 |
| 5 |
| π |
| 6 |
| A、5π | ||
B、
| ||
| C、．2π | ||
D、
|
已知a∥α，b?α，则直线a与直线b的位置关系是（ ）
| A、平行 | B、平行或异面 |
| C、相交或异面 | D、异面 |
设 a=sin(-810°)，b=tan(-
)，c=lge，则它们的大小关系为（ ）
| 33π |
| 8 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜c＜a |
| D、c＜a＜b |