题目内容
5.已知P(x,y)是圆(x+1)2+y2=1上一点,则2x+3y的最大值为$\sqrt{13}$-2.分析 假设点P的坐标为(-1+cosα,sinα),利用三角函数,可求最值.
解答 解:圆的标准方程为(x+1)2+y2=1,
设P(-1+cosα,sinα),则
2x+3y=2cosα+3sinα-2=$\sqrt{13}$cos(α+θ)-2
∴2x+3y的最大值为:$\sqrt{13}$-2.
故答案为:$\sqrt{13}$-2.
点评 本题以圆为载体,考查圆的标准方程,考查函数的最值,关键是利用三角函数假设变量.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
13.已知函数f(x)=e2-x+x,x∈[1,3],则下列说法正确的是( )
| A. | 函数f(x)的最大值为$3+\frac{1}{e}$ | B. | 函数f(x)的最小值为$3+\frac{1}{e}$ | ||
| C. | 函数f(x)的最大值为3 | D. | 函数f(x)的最小值为3 |
10.将正奇数按如下规律填在5列的数表中:则2015排在该表的第252行,第1列.(行是从上往下数,列是从左往右数).
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |
17.成书于公元五世纪的《张邱建算经》是中国古代数学史上的杰作,该书中记载有很多数列问题,说明古人很早就注意到了数列并且有很深的研究,从下面这首古民谣中可知一二:
南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸①,头圈一尺三②.
逐节多三分③,逐圈少分三④.一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?
此民谣提出的问题的答案是( )
(注:①五寸即0.5尺.②一尺三即1.3尺.③三分即0.03尺.④分三即一分三厘,等于0.013尺.)
南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸①,头圈一尺三②.
逐节多三分③,逐圈少分三④.一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?
此民谣提出的问题的答案是( )
(注:①五寸即0.5尺.②一尺三即1.3尺.③三分即0.03尺.④分三即一分三厘,等于0.013尺.)
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
15.设集合A={x|x2-9<0},B={x|2x∈N},则A∩B的元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
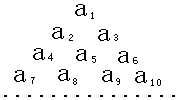 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.