题目内容
数列{an}满足a1=2,an=
,其前n项积为Tn,则T2015=( )
| an+1-1 |
| an+1+1 |
| A、2 | B、1 | C、3 | D、-6 |
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:根据数列{an}满足a1=2,an=
,可得数列{an}是周期为4的周期数列,且T4=a1a2a3a4=1,即可得出结论.
| an+1-1 |
| an+1+1 |
解答:
解:∵a1=2,an=
,
∴a1=
=2,解得a2=-3,
则
=a2=-3,解得a3=-
,
则
=a3=-
,解得a4=
,
则
=a4=
,解得a5=2,
…,
则an的取值具备周期性,周期数为4,
且T4=a1a2a3a4=-3×(-
)×
×2=1,
则T2015=a1a2a3a4…a2015=a1a2a3═2×(-3)×(-
)=3.
故选:C
| an+1-1 |
| an+1+1 |
∴a1=
| a2-1 |
| a2+1 |
则
| a3-1 |
| a3+1 |
| 1 |
| 2 |
则
| a4-1 |
| a4+1 |
| 1 |
| 2 |
| 1 |
| 3 |
则
| a5-1 |
| a5+1 |
| 1 |
| 3 |
…,
则an的取值具备周期性,周期数为4,
且T4=a1a2a3a4=-3×(-
| 1 |
| 2 |
| 1 |
| 3 |
则T2015=a1a2a3a4…a2015=a1a2a3═2×(-3)×(-
| 1 |
| 2 |
故选:C
点评:本题考查数列递推式,考查学生分析解决问题的能力,确定数列{an}是周期为4的周期数列,且T4=a1a2a3a4=1,是关键.

练习册系列答案
相关题目
已知向量
=(1,2)与向量
=(
,cosθ)共线,则向量
=(tanθ,-
)的模为( )
| a |
| b |
| ||
| 4 |
| c |
| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
若集合M={y|y=2-x},N={x|y=
},则M∩N等于( )
| x-1 |
| A、{y|y>1} |
| B、{y|y≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
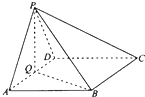 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.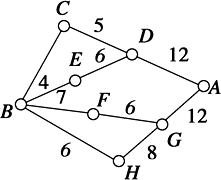 如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为
如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为