Question

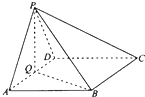如图，四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q是AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）若平面APD⊥平面ABCD，且PA=PD=AD=2，在线段PC上是否存在点M，使二面角M-BQ-C的大小为60°．若存在，试确定点M的位置，若不存在，请说明理由．

Answer 1

考点：与二面角有关的立体几何综合题,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）由已知得PQ⊥AD，BQ⊥AD，由此能证明平面PQB⊥平面PAD．
（2）以Q为坐标原点，分别以QA，QB，QP为x，y，z轴，建立空间直角坐标系，利用向量法能求出存在点M为线段PC靠近P的三等分点满足题意．

解答： （1）证明：∵PA=PD，Q为AD的中点，∴PQ⊥AD，
又∵底面ABCD为菱形，∠BAD=60°，∴BQ⊥AD，
又PQ∩BQ=Q，∴AD⊥平面PQB，
又∵AD?平面PAD，
∴平面PQB⊥平面PAD．
（2）解：∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PQ⊥AD，
∴PQ⊥平面ABCD，
以Q为坐标原点，分别以QA，QB，QP为x，y，z轴，
建立空间直角坐标系，如图
则Q（0，0，0），P（0，0，

3

），B（0，

3

，0），C（-2，

3

，0）
设

PM

=λ

PC

，0＜λ＜1，则M（-2λ，

3

λ，

3

(1-λ)），
平面CBQ的一个法向量

n1

=（0，0，1），
设平面MBQ的法向量为

n2

=（x，y，z），
由

QM • n2 =0 QB • n2 =0

，得

n2

=（

3-3λ

2λ

，0，

3

），
∵二面角M-BQ-C的大小为60°，
∴cos60°=|cos＜

n1

，

n2

＞|=|

3

( 3-3λ 2λ )2+3

|=

1

2

，
解得λ=

1

3

，∴

PM

PC

=

1

3

，
∴存在点M为线段PC靠近P的三等分点满足题意．

点评：本题考查平面与平面垂直的证明，考查满足条件的点是否存在的判断与证明，解题时要认真审题，注意空间思维能力的培养．