题目内容
已知y=f(x)为R上的连续可导函数,当x≠0时,f(x)+
>0,则关于x的函数g(x)=f(x)+
的零点的个数为( )
| f(x) |
| x |
| 1 |
| x |
| A、1 | B、0 | C、2 | D、0或2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用,导数的概念及应用
分析:由题意可得,x≠0,因而 g(x)的零点跟 xg(x)的非零零点是完全一样的.当x>0时,利用导数的知识可得xg(x)在(0,+∞)上是递增函数,xg(x)>1恒成立,可得xg(x)在(0,+∞)上无零点.同理可得xg(x)在(-∞,0)上也无零点,从而得出结论.
解答:
解:由于函数g(x)=f(x)+
,可得x≠0,
因而 g(x)的零点跟 xg(x)的非零零点是完全一样的,
故我们考虑 xg(x)=xf(x)+1 的零点.
由于当x≠0时,f(x)+
>0,
①当x>0时,(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x( f′(x)+
)>0,
所以,在(0,+∞)上,函数x•g(x)单调递增函数.
又∵
[xf(x)+1]=1,
∴在(0,+∞)上,
函数 x•g(x)=xf(x)+1>1恒成立,
因此,在(0,+∞)上,函数 x•g(x)=xf(x)+1 没有零点.
②当x<0时,由于(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x( f′(x)+
)<0,
②当x<0时,由于(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x( f′(x)+
)<0,
故函数 x•g(x)在(-∞,0)上是递减函数,函数 x•g(x)=xf(x)+1>1恒成立,
故函数 x•g(x)在(-∞,0)上无零点.
综上可得,函g数(x)=f(x)+
在R上的零点个数为0,
故选:B
| 1 |
| x |
因而 g(x)的零点跟 xg(x)的非零零点是完全一样的,
故我们考虑 xg(x)=xf(x)+1 的零点.
由于当x≠0时,f(x)+
| f(x) |
| x |
①当x>0时,(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x( f′(x)+
| f(x) |
| x |
所以,在(0,+∞)上,函数x•g(x)单调递增函数.
又∵
| lim |
| x→0 |
∴在(0,+∞)上,
函数 x•g(x)=xf(x)+1>1恒成立,
因此,在(0,+∞)上,函数 x•g(x)=xf(x)+1 没有零点.
②当x<0时,由于(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x( f′(x)+
| f(x) |
| x |
②当x<0时,由于(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x( f′(x)+
| f(x) |
| x |
故函数 x•g(x)在(-∞,0)上是递减函数,函数 x•g(x)=xf(x)+1>1恒成立,
故函数 x•g(x)在(-∞,0)上无零点.
综上可得,函g数(x)=f(x)+
| 1 |
| x |
故选:B
点评:本题考察了函数的单调性,导数的应用,函数的零点,属中档题.

练习册系列答案
相关题目
数列{an}满足a1=2,an=
,其前n项积为Tn,则T2015=( )
| an+1-1 |
| an+1+1 |
| A、2 | B、1 | C、3 | D、-6 |
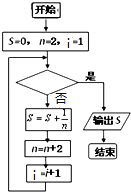 如图所示给出的是计算
如图所示给出的是计算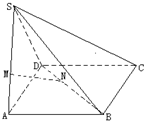 如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且
如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且