题目内容
已知圆x2+y2-x=0与直线x+y-1=0交于P,Q两点,动圆C过P,Q两点.
(1)若圆C圆心在直线y=
x上,求圆C的方程;
(2)求动圆C的面积的最小值;
(3)若圆C与x轴相交于两点M,N(点N横坐标大于1).若过点M任作的一条与圆O:x2+y2=4交于A,B两点直线都有∠ANM=∠BNM,求圆C的方程.
(1)若圆C圆心在直线y=
| 1 |
| 2 |
(2)求动圆C的面积的最小值;
(3)若圆C与x轴相交于两点M,N(点N横坐标大于1).若过点M任作的一条与圆O:x2+y2=4交于A,B两点直线都有∠ANM=∠BNM,求圆C的方程.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)由题意可设圆C方程为x2+y2-x+λ(x+y-1)=0,圆C圆心在直线y=
x上即可得出λ.
(2)由(1)可得r2=
(λ+
)2+
≥
,即可得出动圆C的面积的最小值.
(3)设圆C方程为x2+y2-x+λ(x+y-1)=0,令y=0,x2+(λ-1)x-λ=0,可得xM=1,xN=-λ,-λ>1.设直线AB的方程为y=k(x-1),代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,设A(x1,y1),B(x2,y2),可得根与系数的关系,由于∠ANM=∠BNM,可得
+
=0,代入解出即可.
| 1 |
| 2 |
(2)由(1)可得r2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
(3)设圆C方程为x2+y2-x+λ(x+y-1)=0,令y=0,x2+(λ-1)x-λ=0,可得xM=1,xN=-λ,-λ>1.设直线AB的方程为y=k(x-1),代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,设A(x1,y1),B(x2,y2),可得根与系数的关系,由于∠ANM=∠BNM,可得
| y1 |
| x1+λ |
| y2 |
| x2+λ |
解答:
解:(1)设圆C方程为x2+y2-x+λ(x+y-1)=0,
(x-
)2+(y+
)2=
.
∵-
=
×
,解得λ=-1.
∴圆C方程为x2+y2-2x-y+1=0.
(2)由(1)可得r2=
(λ+
)2+
≥
,∴动圆C的面积的最小值为
π.
(3)设圆C方程为x2+y2-x+λ(x+y-1)=0,
令y=0,x2+(λ-1)x-λ=0,
∴(x-1)(x+λ)=0,xM=1,xN=-λ,-λ>1.
设直线AB的方程为y=k(x-1),
代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,
设A(x1,y1),B(x2,y2),从而x1+x2=
,x1x2=
.
∵
+
=
,
而(x1-1)(x2+λ)+(x2-1)(x1+λ)
=2x1x2-(-λ+1)(x2+x1)-2λ=2
-(-λ+1)
-2λ=
,
∵∠ANM=∠BNM,
∴
+
=0,即
=0,得λ=-4.
当直线AB与x轴垂直时也成立.
∴圆C的方程为x2-5x+y2-4y+4=0.
(x-
| 1-λ |
| 2 |
| λ |
| 2 |
| 2λ2+2λ+1 |
| 4 |
∵-
| λ |
| 2 |
| 1 |
| 2 |
| 1-λ |
| 2 |
∴圆C方程为x2+y2-2x-y+1=0.
(2)由(1)可得r2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
(3)设圆C方程为x2+y2-x+λ(x+y-1)=0,
令y=0,x2+(λ-1)x-λ=0,
∴(x-1)(x+λ)=0,xM=1,xN=-λ,-λ>1.
设直线AB的方程为y=k(x-1),
代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,
设A(x1,y1),B(x2,y2),从而x1+x2=
| 2k2 |
| 1+k2 |
| k2-4 |
| 1+k2 |
∵
| y1 |
| x1+λ |
| y2 |
| x2+λ |
| k[(x1-1)(x2+λ)+(x2-1)(x1+λ)] |
| (x1+λ)(x2+λ) |
而(x1-1)(x2+λ)+(x2-1)(x1+λ)
=2x1x2-(-λ+1)(x2+x1)-2λ=2
| k2-4 |
| 1+k2 |
| 2k2 |
| 1+k2 |
| 2λ-8 |
| 1+k2 |
∵∠ANM=∠BNM,
∴
| y1 |
| x1+λ |
| y2 |
| x2+λ |
| 2λ-8 |
| 1+k2 |
当直线AB与x轴垂直时也成立.
∴圆C的方程为x2-5x+y2-4y+4=0.
点评:本题考查了直线与圆的相交问题转化为方程联立可得根与系数的关系、圆的标准方程及其性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
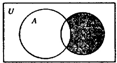 设集合U={1,2,3,4,5},A={1,2,3},B={2,4},则图中阴影部分所表示的集合是( )
设集合U={1,2,3,4,5},A={1,2,3},B={2,4},则图中阴影部分所表示的集合是( )| A、{1,3,4} |
| B、{2,4} |
| C、{4,5} |
| D、{4} |
已知O为空间直角坐标系的原点,以下能使向量
,
,
共面的三点A,B,C的坐标是( )
| OA |
| OB |
| OC |
| A、A(1,0,0),B(0,1,0),C(0,0,1) |
| B、A(1,2,3),B(3,0,2),C(4,2,5) |
| C、A(1,1,0),B(1,0,1),C(0,1,1) |
| D、A(1,1,1),B(1,1,0),C(1,0,1) |
数列{an}满足a1=2,an=
,其前n项积为Tn,则T2015=( )
| an+1-1 |
| an+1+1 |
| A、2 | B、1 | C、3 | D、-6 |
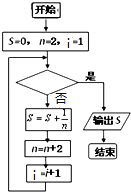 如图所示给出的是计算
如图所示给出的是计算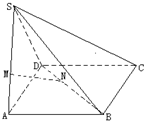 如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且
如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且