题目内容
函数f（x）=
的定义域为 ．
| ||
| log2(x-1) |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据使函数f（x）=
的解析式有意义，得到不等式组：
，解得答案．
| ||
| log2(x-1) |
|
解答：
解：若使函数f（x）=
的解析式有意义，
自变量x须满足：
，
解得：x∈[3，+∞），
故函数f（x）=
的定义域为[3，+∞），
故答案为：[3，+∞）
| ||
| log2(x-1) |
自变量x须满足：
|
解得：x∈[3，+∞），
故函数f（x）=
| ||
| log2(x-1) |
故答案为：[3，+∞）
点评：求函数的定义域时要注意：（1）当函数是由解析式给出时，其定义域是使解析式有意义的自变量的取值集合．（2）当函数是由实际问题给出时，其定义域的确定不仅要考虑解析式有意义，还要有实际意义（如长度、面积必须大于零、人数必须为自然数等）．（3）若一函数解析式是由几个函数经四则运算得到的，则函数定义域应是同时使这几个函数有意义的不等式组的解集．若函数定义域为空集，则函数不存在．（4）对于（4）题要注意：①对在同一对应法则f 下的量“x”“x+a”“x-a”所要满足的范围是一样的；②函数g（x）中的自变量是x，所以求g（x）的定义域应求g（x）中的x的范围．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图，在矩形ABCD中，AB=2，BC=
，E是CD的中点，那么
•
=（ ）
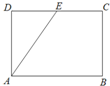
| 3 |
| AE |
| DC |
| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
已知函数f（x）是定义在R上的奇函数，当x∈（-∞，0）时，有xf′（x）＜f（-x）成立．（其中f′（x）是f（x）的导函数），若a=
f（
），b=f（1），c=log2
f（log2
）则a，b，c的大小关系是（ ）
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、a＞b＞c |
| B、c＞b＞a |
| C、b＞a＞c |
| D、c＞a＞b |
设命题p：?平面向量
和
，|
-
|＜|
|+|
|，则?p为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、?平面向量
| ||||||||||||
B、?平面向量
| ||||||||||||
C、?平面向量
| ||||||||||||
D、?平面向量
|
设x，y满足约束条件
，则z=x+2y的最大值是（ ）
|
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|
从数字1，2，3，4，5中，任意取出两个数字，不是连续的自然数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|