题目内容

设命题p：?平面向量
a
和
b
，|
a
-
b
|＜|
a
|+|
b
|，则?p为（　　）
A、?平面向量
a
和
b
，|
a
-
b
|≥|
a
|+|
b
|
B、?平面向量
a
和
b
，|
a
-
b
|＜|
a
|+|
b
|
C、?平面向量
a
和
b
，|
a
-
b
|＞|
a
|+|
b
|
D、?平面向量
a
和
b
，|
a
-
b
|≥|
a
|+|
b
|
考点：平面向量数量积的运算
专题：平面向量及应用,简易逻辑
分析：由命题的否定的定义知命题p：?平面向量
a
和
b
，|
a
-
b
|＜|
a
|+|
b
|，则?p：?平面向量
a
和
b
，|
a
-
b
|≥|
a
|+|
b
|．
解答： 解：由?平面向量
a
和
b
的否定为：?平面向量
a
和
b
，
|
a
-
b
|＜|
a
|+|
b
|的否定为：|
a
-
b
|≥|
a
|+|
b
|．
即有命题p：?平面向量
a
和
b
，|
a
-
b
|＜|
a
|+|
b
|，
则?p：?平面向量
a
和
b
，|
a
-
b
|≥|
a
|+|
b
|．
故选D．
点评：本题考查命题的否定，解题时要熟练掌握基本定义．
练习册系列答案
相关题目
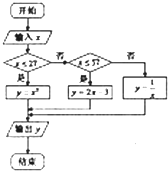若程序框图如图所示，视x为自变量，y为函数值，可得函数y=f（x）的解析式，那么函数f（x）-4在x∈R上的零点个数为（　　）
A、2B、3C、4D、5
直线
x=t+1
y=2t+3
（t为参数）与圆
x=
5
cosθ+2
y=
5
sinθ
（θ为参数）的位置关系为
 
．
若{（x，y）|
x-2y+5≥0
3-x≥0
x+y≥0
}⊆{（x，y）|x2+y2≤m2（m＞0）}，则实数m的取值范围是
 
．
已知集合M={x|x≥0}，P={0，1，2}，则有（　　）
A、M?PB、M⊆P
C、M∩P=MD、M∩P=∅
函数f（x）=
|x-2|-1
log2(x-1)
的定义域为
 
．
设实数x，y满足
2x+y≥0
x-y≥0
0≤x≤k
，若z=x+2y的最大值为18，则z的最小值为
 
．
在△ABC中，角A、B、C的对边分别为a、b、c．
（I）设
m
=（a，cosB），
n
=（b，cosA），当a≠b且
m
∥
n
时，判断△ABC的形状；
（Ⅱ）若4sin2
A+B
2
-cos2C=
7
2
_ ，且c=
7
，求△ABC面积的最大值．
在△ABC中，D是BC的中点，则
AD
=（　　）
A、
1
2
(
AB
+
AC
)
B、
1
2
(
AB
-
AC
)
C、
1
2
(
AB
+
BC
)
D、
1
2
(
AB
-
BC
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网