题目内容
7.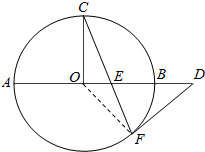 如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.(1)求证:DE2=DB•DA;
(2)若DB=2,DF=4,试求CE的长.
分析 (1)连接OF,利用切线的性质及角之间的互余关系得到DF=DE,再结合切割线定理证明DE2=DB•DA,即可求出DE.
(2)求出BE=2,OE=1,利用勾股定理求CE的长.
解答 (1)证明:连接OF.
因为DF切⊙O于F,所以∠OFD=90°.
所以∠OFC+∠CFD=90°.
因为OC=OF,所以∠OCF=∠OFC.
因为CO⊥AB于O,所以∠OCF+∠CEO=90°.
所以∠CFD=∠CEO=∠DEF,所以DF=DE.
因为DF是⊙O的切线,所以DF2=DB•DA.
所以DE2=DB•DA.
(2)解:∵DF2=DB•DA,DB=2,DF=4.
∴DA=8,从而AB=6,则OC=3.
又由(1)可知,DE=DF=4,∴BE=2,OE=1.
从而 在Rt△COE中,$CE=\sqrt{C{O^2}+O{E^2}}=\sqrt{10}$.
点评 本题主要考查了与圆有关的比例线段、圆的切线的性质定理的应用,属于中档题.

练习册系列答案
相关题目
12.过双曲线一焦点且垂直于双曲线实轴的直线交双曲线于A、B两点,若以AB为直径的圆恰过双曲线的一个顶点,则双曲线的离心率是( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\sqrt{3}$ | D. | 2 |
2.已知f(x)=2|x|+x2+a-1有唯一的零点,则实数a的值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
12.设集合A=$\left\{{x|y=\sqrt{x-1}}\right\}$,集合B=$\left\{{y|y={{log}_2}x,x∈[{\frac{1}{2},4}]}\right\}$,则A∩B=( )
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
16.下列函数中,既是偶函数又存在零点的是( )
| A. | y=x3 | B. | y=ex | C. | y=x2+1 | D. | y=ln|x| |
 P为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1上任意一点,F1,F2为左、右焦点,如图所示.
P为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1上任意一点,F1,F2为左、右焦点,如图所示.