题目内容
13.已知0<x<1,函数f(x)=(1+x2)(2-x),(1)求函数f(x)的最小值;
(2)若a、b、c为正,且满足a+b+c=1,求证$\frac{1}{1+{a}^{2}}$+$\frac{1}{1+{b}^{2}}$+$\frac{1}{1+{c}^{2}}$≤$\frac{27}{10}$.
分析 (1)f(x)=(1+x2)(2-x)=-x3+2x2-x+2,0<x<1,可得f′(x)=-3x2+4x-1=-(3x-1)(x-1),利用导数研究函数的单调性极值即可得出.
(2)由(1)可得:0<x<1,(1+x2)(2-x)≥$\frac{50}{27}$,$\frac{1}{1+{x}^{2}}$≤$\frac{27(2-x)}{50}$.利用a、b、c为正,且满足a+b+c=1,代入即可得出.
解答 (1)解:f(x)=(1+x2)(2-x)=-x3+2x2-x+2,0<x<1,
f′(x)=-3x2+4x-1=-(3x-1)(x-1),
当$0<x<\frac{1}{3}$时,f′(x)<0,此时函数f(x)单调递减;当$\frac{1}{3}<x<1$时,f′(x)>0,此时函数f(x)单调递增.
∴当x=$\frac{1}{3}$时,函数f(x)取得极小值即最小值,$f(\frac{1}{3})$=$(1+\frac{1}{9})$×$(2-\frac{1}{3})$=$\frac{50}{27}$.
(2)证明:由(1)可得:0<x<1,(1+x2)(2-x)≥$\frac{50}{27}$,∴$\frac{1}{1+{x}^{2}}$≤$\frac{27(2-x)}{50}$.
∵a、b、c为正,且满足a+b+c=1,
∴$\frac{1}{1+{a}^{2}}$+$\frac{1}{1+{b}^{2}}$+$\frac{1}{1+{c}^{2}}$≤$\frac{27[6-(a+b+c)]}{50}$=$\frac{27}{10}$.当且仅当a=b=c=$\frac{1}{3}$时取等号.
∴$\frac{1}{1+{a}^{2}}$+$\frac{1}{1+{b}^{2}}$+$\frac{1}{1+{c}^{2}}$≤$\frac{27}{10}$.
点评 本题考查了利用导数研究函数的单调性极值并且证明不等式,考查了推理能力与计算能力,属于中档题.

| A. | {bn}一定为等比数列 | B. | {bn}一定为等差数列 | ||
| C. | 从第二项起{bn}一定为等比数列 | D. | 从第二项起{bn}一定为等差数列 |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |
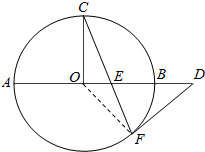 如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.