题目内容
17. P为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1上任意一点,F1,F2为左、右焦点,如图所示.
P为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1上任意一点,F1,F2为左、右焦点,如图所示.(1)若PF1的中点为M,求证:MO=5-$\frac{1}{2}$|PF1|;
(2)若∠F1PF2=60°,求|PF1|•|PF2|的值以及△PF1F2的面积;
(3)椭圆上是否存在点P,使$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,若存在,求出P点的坐标,若不存在,试说明理由.
分析 (1)在△F1PF2中,MO为中位线,根据三角形的中位线定理再结合椭圆的定义即可得出答案;
(2)先利用椭圆的定义得到:|PF1|+|PF2|=10,再在△PF1F2中利用余弦定理得出cos 60°=$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$,两者结合即可求得|PF1|•|PF2|,由三角形面积公式即可得解;
(3)先设点P(x0,y0),根据椭圆的性质,易知F1(-3,0),F2(3,0),写出向量的坐标再结合向量垂直的条件得出关于P点坐标的方程组,由此方程组无解,故这样的点P不存在.
解答  证明:(1)在△F1PF2中,MO为中位线,
证明:(1)在△F1PF2中,MO为中位线,
∴|MO|=$\frac{|P{F}_{2}|}{2}$=$\frac{2a-|P{F}_{1}|}{2}$
=a-$\frac{|P{F}_{1}|}{2}$=5-$\frac{1}{2}$|PF1|.….(3分)
(2)解:∵|PF1|+|PF2|=10,
∴|PF1|2+|PF2|2=100-2|PF1|•|PF2|,
在△PF1F2中,cos 60°=$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$,
∴|PF1|•|PF2|=100-2|PF1|•|PF2|-36,
∴|PF1|•|PF2|=$\frac{64}{3}$.…(8分)
∴${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$×|PF1|×|PF2|×sin60°=$\frac{16\sqrt{3}}{3}$.…(9分)
(3)解:设点P(x0,y0),则 $\frac{{{x}_{0}}^{2}}{25}+\frac{{{y}_{0}}^{2}}{16}=1$.①
易知F1(-3,0),F2(3,0),故$\overrightarrow{P{F}_{1}}$=(-3-x0,-y0),$\overrightarrow{P{F}_{2}}$=(3-x0,-y0),
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
∴x${{\;}_{0}}^{2}$-9+y${{\;}_{0}}^{2}$=0,②
由①②组成方程组,此方程组无解,故这样的点P不存在. …(12分)
点评 本小题主要考查椭圆的标准方程、椭圆的简单性质、解三角形等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基本知识的考查.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
| A. | 1 | B. | $\frac{1}{2}$或$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
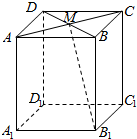 在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
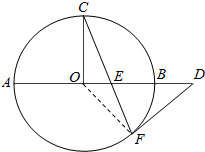 如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E. 已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),
已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),