题目内容
12.过双曲线一焦点且垂直于双曲线实轴的直线交双曲线于A、B两点,若以AB为直径的圆恰过双曲线的一个顶点,则双曲线的离心率是( )| A. | $\frac{3}{2}$ | B. | 3 | C. | $\sqrt{3}$ | D. | 2 |
分析 先求出A的坐标,利用以AB为直径的圆恰过双曲线的一个顶点,可得$\frac{{b}^{2}}{a}$=c+a,从而可求双曲线的离心率.
解答 解:不妨设A(c,y0),代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得y0=±$\frac{{b}^{2}}{a}$.
∵以AB为直径的圆恰过双曲线的一个顶点,
∴$\frac{{b}^{2}}{a}$=c+a,
∴ac+a2=b2,
∴e2-e-2=0,
∵e>1,
∴e=2.
故选:D.
点评 本题考查双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
1.己知数列{cn}的前n项和为Tn,若数列{cn}满足各项均为正项,并且以(cn,Tn)(n∈N*)为坐标的点都在曲线ay=$\frac{a}{2}$x2+$\frac{a}{2}$x+b,(a为非0常数)上运动,则称数列{cn}为“抛物数列”,己知数列{bn}为“抛物数列”,则( )
| A. | {bn}一定为等比数列 | B. | {bn}一定为等差数列 | ||
| C. | 从第二项起{bn}一定为等比数列 | D. | 从第二项起{bn}一定为等差数列 |
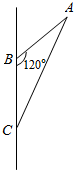 如图所示,在△ABC中,AB=2,BC=2,∠ABC=120°,若将△ABC绕BC旋转一周,求所形成的旋转体的表面积和体积.
如图所示,在△ABC中,AB=2,BC=2,∠ABC=120°,若将△ABC绕BC旋转一周,求所形成的旋转体的表面积和体积.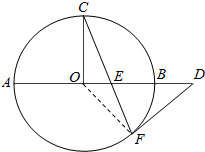 如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.