题目内容
10.甲、乙两人自相距27千米处相向出发,甲匀速行进,每小时4千米,乙第一小时走2千米,以后每小时多走0.5千米,问几小时甲、乙相遇?分析 设经过x小时甲、乙相遇,由题意和等差数列的求和公式解得x的方程,解x可得.
解答 解:设经过x小时甲、乙相遇,此时甲走了4x千米,
乙走了2x+$\frac{x(x-1)}{2}$×0.5千米,
由题意可得4x+2x+$\frac{x(x-1)}{2}$×0.5=27,
解方程可得x=4,或x=-23(舍去)
故经过4小时甲、乙相遇.
点评 本题考查函数解析式的求解,涉及等差数列的求和公式,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.己知数列{cn}的前n项和为Tn,若数列{cn}满足各项均为正项,并且以(cn,Tn)(n∈N*)为坐标的点都在曲线ay=$\frac{a}{2}$x2+$\frac{a}{2}$x+b,(a为非0常数)上运动,则称数列{cn}为“抛物数列”,己知数列{bn}为“抛物数列”,则( )
| A. | {bn}一定为等比数列 | B. | {bn}一定为等差数列 | ||
| C. | 从第二项起{bn}一定为等比数列 | D. | 从第二项起{bn}一定为等差数列 |
18.已知三个集合A、B、C,则“A⊆B,B⊆C,C⊆A”是“A=B=C”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |
4.已知实数x,y满足$\left\{\begin{array}{l}x≤3\\ y≤4\\ 4x+3y-12≥0\end{array}\right.$则z=x2+y2的取值范围是( )
| A. | [3,5] | B. | [9,25] | C. | $[\frac{12}{5},5]$ | D. | $[\frac{144}{25},25]$ |
5.在△ABC中,若sinC(cosA+cosB)=sinA+sinB,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
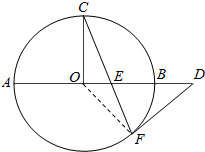 如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.