题目内容
已知函数f(x)=lnx-
+(a-1)x-
,其中a>0
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个相异的零点x1,x2,求实数a的取值范围.
| ax2 |
| 2 |
| 3 |
| 2a |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个相异的零点x1,x2,求实数a的取值范围.
考点:三角函数中的恒等变换应用,函数零点的判定定理
专题:导数的综合应用
分析:(Ⅰ)对函数f(x)进行求导,令导函数大于0求得x的范围.
(Ⅱ)先根据导函数判断函数的单调性及函数的最大值,进而推断出函数的最大值大于0即可出现两个相异的零点,进而取得a的范围.
(Ⅱ)先根据导函数判断函数的单调性及函数的最大值,进而推断出函数的最大值大于0即可出现两个相异的零点,进而取得a的范围.
解答:
解:(Ⅰ)f′(x)=
-ax+a-1=-
,
当0<x<1时,f′(x)>0,
∴函数的单调增区间为(0,1).
(Ⅱ)由(Ⅰ)知当0<x<1时,f′(x)>0,函数单调增
当x>1或x<0时,f′(x)<0,函数单调减,
x=1时,f′(x)=0,函数f(x)求得极值,
∴f(1)为函数f(x)的最大值,
∴要使函数f(x)有两个相异的零点x1,x2,
需f(1)>0,
即ln1-
+a-1-
>0,整理得
>0,
求得a>3或-1<a<0.
| 1 |
| x |
| (x-1)(a+1) |
| x |
当0<x<1时,f′(x)>0,
∴函数的单调增区间为(0,1).
(Ⅱ)由(Ⅰ)知当0<x<1时,f′(x)>0,函数单调增
当x>1或x<0时,f′(x)<0,函数单调减,
x=1时,f′(x)=0,函数f(x)求得极值,
∴f(1)为函数f(x)的最大值,
∴要使函数f(x)有两个相异的零点x1,x2,
需f(1)>0,
即ln1-
| a |
| 2 |
| 3 |
| 2a |
| (a-3)(a+1) |
| 2a |
求得a>3或-1<a<0.
点评:本题主要考查了导函数的综合运用.对导数公式要熟练记忆,通过导函数大于0和小于0判断函数的单调性,是导函数常用方法.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
过点P(3,2),且在两坐标轴上的截距相等的直线方程为( )
| A、2x-3y=0 |
| B、x+y-6=0 |
| C、x+y-5=0 |
| D、2x-3y=0或x+y-5=0 |
 如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,
如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,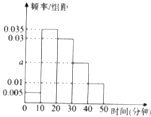 经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.
经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.