题目内容
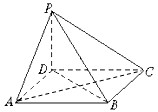 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.(1)求证:平面PAC⊥平面PBD;
(2)求PC与平面PBD所成的角.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得AC⊥PD,由正方形性质得AC⊥BD,由此能证明平面PAC⊥平面PBD.
(2)记AC与BD相交于O,连结PO,由已知条件得∠CPO就是PC与平面PBD所成的角,由此能求出PC与平面PBD所成的角为30°.
(2)记AC与BD相交于O,连结PO,由已知条件得∠CPO就是PC与平面PBD所成的角,由此能求出PC与平面PBD所成的角为30°.
解答:
 (1)证明:∵PD⊥底面ABCD,AC?底面ABCD,
(1)证明:∵PD⊥底面ABCD,AC?底面ABCD,
∴AC⊥PD,
又∵底面ABCD为正方形,
∴AC⊥BD,而PD与BD交于点D,
∴AC⊥平面PBD,…(4分)
又AC?平面PAC,
∴平面PAC⊥平面PBD.…(6分)
(2)解:记AC与BD相交于O,连结PO,
由(1)知,AC⊥平面PBD,
∴PC在平面PBD内的射影是PO,
∴∠CPO就是PC与平面PBD所成的角,…(10分)
∵PD=AD,
∴在Rt△PDC中,PC=
CD,
而在正方形ABCD中,OC=
AC=
CD,
∴在Rt△POC中,有∠CPO=30°.
即PC与平面PBD所成的角为30°.…(14分)
 (1)证明:∵PD⊥底面ABCD,AC?底面ABCD,
(1)证明:∵PD⊥底面ABCD,AC?底面ABCD,∴AC⊥PD,
又∵底面ABCD为正方形,
∴AC⊥BD,而PD与BD交于点D,
∴AC⊥平面PBD,…(4分)
又AC?平面PAC,
∴平面PAC⊥平面PBD.…(6分)
(2)解:记AC与BD相交于O,连结PO,
由(1)知,AC⊥平面PBD,
∴PC在平面PBD内的射影是PO,
∴∠CPO就是PC与平面PBD所成的角,…(10分)
∵PD=AD,
∴在Rt△PDC中,PC=
| 2 |
而在正方形ABCD中,OC=
| 1 |
| 2 |
| ||
| 2 |
∴在Rt△POC中,有∠CPO=30°.
即PC与平面PBD所成的角为30°.…(14分)
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
光线从点A(-3,4)发出,经过x轴反射,再经过y轴反射,最后光线经过点B(-2,6),则经y轴反射的光线的方程为( )
| A、2x+y-2=0 |
| B、2x-y+2=0 |
| C、2x+y+2=0 |
| D、2x-y-2=0 |
 如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,
如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,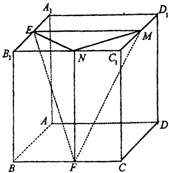 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.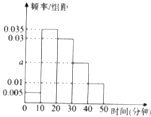 经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.
经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.